The Direct Approach
Empirical scaling laws can help predict the cross-entropy loss associated with training inputs, such as compute and data. However, in order to predict when AI will achieve some subjective level of performance, it is necessary to devise a way of interpreting the cross-entropy loss of a model. This blog post provides a discussion of one such theoretical method, which we call the Direct Approach.
Published
Resources
Overview
Empirical scaling laws can help predict the cross-entropy loss associated with training inputs, such as compute and data. However, in order to predict when AI will achieve some subjective level of performance, we need to interpret the cross-entropy loss of a model. This blog post discusses one such theoretical method, which we call the Direct Approach. The key to understanding the Direct Approach is that scaling laws can be used to forecast KL divergence of the true distribution from the model, which can in turn tell us how distinguishable the model is from the true distribution. Arguably, indistinguishability over sufficiently long sequences implies competence on the tasks implicit in the data distribution; if true, we can use scaling laws to upper bound the training compute necessary to achieve a particular level of performance.
The Direct Approach is our name for the idea of forecasting AI timelines by directly extrapolating and interpreting the loss of machine learning models as described by scaling laws. The basic idea is that we can interpret a model’s cross-entropy loss as determining “how distinguishable” the model is from its training distribution, and we can use that quantity to upper bound the difficulty of training a model to perform reliable, high-quality reasoning over long sequences.
The full approach is described in a report, which can be found here.
The approach comes from noticing that cross-entropy can be interpreted mathematically as a measure of how well a model can emulate its training distribution. If a model is capable of perfectly emulating some task, then its cross-entropy loss should be equal to the irreducible loss. In that case, it is easy to see how we could substitute the model for a human performing that task with no loss in performance.
The primary insight here is that indistinguishability implies competence: if you can’t tell whether a set of outputs comes from the model or from humans, then the model should be at least as competent as the humans performing the same task. Of course, in the real world, no models achieve the irreducible loss on any complex distribution. Therefore, it is necessary to devise a framework for answering what level of reducible loss is “good enough” to perform adequately on whatever task we want to automate.
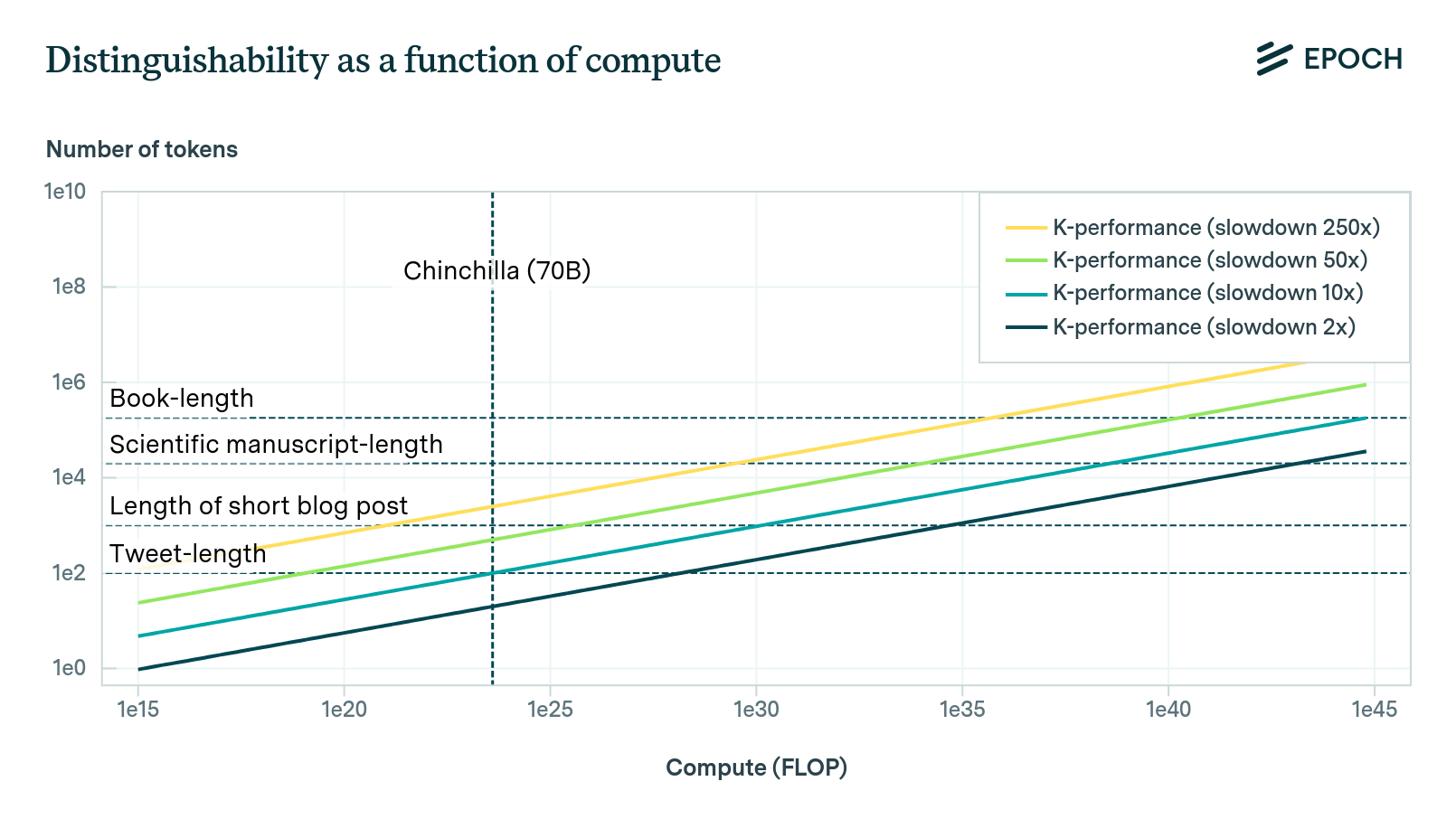
Our approach to this question takes advantage of the properties of the KL divergence, which we can estimate using scaling laws. The idea is that KL divergence of the training distribution from the model tells us how many samples it takes from the model, on average, before we can reach a desired level of confidence about whether we are sampling from the model or the true distribution. We call this quantity the “k-performance” of the model.
The k-performance of a model is actually derived from two principles, the first being a trivial property of the KL divergence, and the second being a model of human discrimination abilities. The KL divergence directly tells how many samples it should take an ideal observer, on average, before it’s able to distinguish the model from the training distribution. But in practice, this quantity will likely be far lower than the actual number of samples that it takes a trained human judge to do the same.
In the report, I introduce a simple model of human discrimination abilities by showing that two models of human abilities imply basically the same result. The first model assumes that humans update slower than an ideal discriminator by a constant factor. The second model assumes that humans only attend to a constant fraction of the evidence that they could theoretically attend to. Both imply that, for any fixed level of performance, the k-performance of a model with respect to a human judge will be some constant multiple of the k-performance of a model with respect to an ideal discriminator, which I call the human slowdown factor.
This result is important because it implies that the k-performance of a model can be calculated using only a scaling law for KL divergence and an estimate of the human slowdown factor; both of these can be estimated via experiment.
On a first approximation, if the k-performance of a model is longer than the average length of a task, then the model can likely substitute for a human worker adequately. That’s because, over lengths shorter than or equal to the average task, it is impossible to confidently determine whether the model’s outputs are from the true distribution or from the model itself. Thus, we should expect that models with a k-performance longer than the average length of a task should be capable of automating the task adequately.
The Direct Approach yields an upper bound on the training compute to automate a task because there may be more efficient ways of getting a model to automate some task than to train the model to emulate humans performing that task directly. Most obviously, at a certain point, the model might be trained more efficiently by directly getting reward signals about how well it’s performing on the task. This is analogous to how a human learning to play tennis might at first try to emulate the skills of good tennis players, but later on develop their own technique by observing what worked and what didn’t work to win matches.
Nonetheless, while the Direct Approach may work in theory, in practice we are very limited on good data that would allow us to calculate a reasonable upper bound on most tasks that we care about. The most salient reason is that the scaling law literature is still thin, and we do not yet have much information about the scaling properties of models that learn on various distributions of interest: for example, mathematics, or scientific literature. The best available data likely comes from Hoffmann et al. (2022), which studied a model that was trained on general internet data. Since we anticipate that the most likely way in which a pure software system could be transformative is if it is capable of automating science, this data limitation provides a severe constraint on our ability to get the Direct Approach to say anything meaningful about the future of AI.
Questions and answers
Moreover, after eliciting feedback about the Direct Approach from many people, we have learned that there are a number of common misunderstandings about the approach that are plausibly worth clearing up systematically, point-by-point. Here is a list of common questions, and our answers to them.
Question: Does this framework make any novel, testable predictions?
Our response: Yes it does! The central prediction of this framework is that there is a linear relationship between the log of training compute for a model (trained compute-optimally), and the number of samples it takes on average for a human to reliably distinguish the model from its training distribution. The framework can be falsified by, for example, showing that it takes 100 tokens on average to reliably distinguish a language model from its training distribution trained with 10^20 FLOP, and 1000 tokens for a model trained with 10^22 FLOP, but only 1200 tokens for a model trained with 10^24 FLOP.
Question: Why assume that a model capable of emulating scientific papers would be capable of doing science, even though it cannot perform experiments in the real world?
Our response: Theoretically, we can apply the Direct Approach to any distribution, meaning that we could use it to calculate the difficulty of training a model to emulate the full scientific process that humans perform, not just the process of writing papers. However, since we lack data about scaling properties on abstract distributions like that, it is way more tractable to use the Direct Approach to bound the difficulty of training a model to emulate ordinary textual documents, like scientific papers.
We tentatively expect the approach to provide useful insight nonetheless because we think that emulating high-quality scientific reasoning is likely to be the hardest bottleneck to getting models to do science. In other words, the Direct Approach could adequately allow us to calculate the upper bound of training a model to perform reliable, high-quality reasoning over long sequences, and if we had such models, they would likely be enormously helpful in automating the scientific process. For example, scientists could query such models and ask what experiments to perform to validate a certain hypothesis.
Question: Why do you assume that scaling laws for internet data will carry over to scaling laws on other tasks, such as scientific reasoning?
Our response: Scaling laws have also been found to be ubiquitous across many different data distributions and modalities (for example, see Henighan et al. 2020).We personally don’t think that non-science internet data is vastly easier to learn than other types of textual data, like scientific papers. State of the art models, like GPT-4, seem to do a decent job at understanding scientific reasoning, despite being trained on non-science internet data. Moreover, progress in non-science language tasks often go hand-in-hand with progress on scientific reasoning abilities. To the extent they fail, it’s often in a way that they’d also fail in a more ordinary setting that one might find on social media (e.g., models fail to make subtle inferences or notice nuanced implications within a given context).
Nonetheless, we think this question represents a reasonable critique of our results, as currently presented. While we do think that scaling laws on more complex distributions, like scientific papers, will look different than the scaling laws in the Chinchilla paper, this does not represent any fatal flaw in the Direct Approach itself, since the method can simply be updated as better data becomes available in the future.
Question: Doesn’t this approach assume that scaling laws will hold over many orders of magnitude. Isn’t that unreasonable?
Our response: We don’t think it’s unreasonable to assume that scaling laws will hold for many orders of magnitude. Scaling laws were anticipated in more or less their current form for decades. For example, the data scaling law in Hoffmann et al. can be seen as an estimate of the convergence rate of gradient descent, which was deduced to have a power law form as early as Nemirovsky et al. (1983). Power law scaling has already been observed over about 24 orders of magnitude of compute, and so expecting it to hold over another 10 or 20 seems reasonable to me.1
Question: Isn’t novel scientific work ‘out of distribution’? The cross-entropy loss on a particular distribution takes an average over a large distribution. However, in practice, what we care about is not the average cross-entropy, but the cross-entropy on a particular subset of the distribution, e.g., the highest quality parts associated with scientific work.
Our response: We agree that what we really care about is the cross-entropy loss of a model on an appropriately complex and useful distribution, like scientific research. However, we expect that with better data on scaling laws, especially scaling laws for transfer, it will become more clear how much we can reduce the cross-entropy loss on certain high-quality tasks that models are not trained on directly, such as scientific research. Furthermore, models can be fine-tuned on high-quality datasets, and we can use the Direct Approach to estimate the training requirements to reach a high performance on those tasks directly. We are already seeing language models acquire a large variety of specific skills even though they are trained on very general distributions. It seems that transfer learning is ubiquitous in this sense.
Question: According to current scaling laws, it takes only a few tokens for an ideal predictor to reliably distinguish between current large language models and the training distribution. Doesn’t that imply that we should put low confidence in these results?
Our response: Yes. The fact that current scaling laws say that an ideal discriminator only needs a few tokens to reliably distinguish between current large language models and their training distribution is a good reason not to put much confidence in these results. More specifically, this fact implies that when we extrapolate performance to much larger models, the error in our estimate will tend to be quite high.
For that reason, we recommend not putting too much trust in any particular bottom line result (like, the idea that we need 10^35 FLOP to train transformative AI). Rather, we think the Direct Approach is better seen as a theoretical framework that can hopefully inform AI timelines, and its utility may increase in the future as we collect more data on scaling, get better language models, and conduct experiments related to human discrimination abilities.
Question: Why do you assume that models will be trained to emulate humans exactly? Won’t we be using some sort of reinforcement learning algorithm to create AGI?
Our response: In general, this approach provides an upper bound on the hardness of learning to perform reliable, high-quality reasoning over long sequences. It does not say that the way we will develop AGI will be by emulating human behavior, though recent developments in language modeling have bolstered that theory, in our opinion. Since emulating human behavior extremely well would be a sufficient condition for “AGI,” this approach seems to yield a plausible upper bound on the difficulty of creating AGI. However, we admit that the upper bound may be too high if we discover a method of creating AGI using less compute or less data.
Question: Why do you assume that a model that gets better at emulating a human will be able to think like a human? Isn’t that kind of like expecting Russell Crowe to get better at game theory the better he’s able to act the role of John Nash?
Our response: This analogy seems to rely on a misleading impression of what language models are actually doing when they learn to write like a human. Unlike what Russell Crowe did to act like John Nash, language models are not just learning how to superficially emulate human personalities. They’re also gradually acquiring the ability to perform reasoning, as indicated by nearly every benchmark that we’ve so far been able to devise. For example, GPT-4 was able to score highly on the MMLU benchmark, a set of 57 high school and college exams.
To refine the analogy, consider if people evaluated Russell Crowe based on not only his portrayal of John Nash’s personality but also his ability to author mathematical papers resembling Nash’s academic work. If Russell Crowe were found to be gradually improving on the task of writing papers that looked very similar to John Nash’s papers, including upon close examination, it would be very reasonable to think that Russell Crowe was actually gradually learning game theory. Fundamentally, this is because to write a paper that reads exactly like a paper from John Nash, it helps to learn game theory first.
Reviews
We asked Nuño Sempere to review this report. His review may be found here. Here’s an excerpt describing his high-level take:
My high level thought is that this is an elegant approach. It warms my blackened heart a bit. I’m curious about why previous attempts, e.g., various reports commissioned by Open Philanthropy, didn’t think of it in some shape.
The review certainly contains many critical responses, and we encourage the reader to read it.
-
A time-invariant version of Laplace’s law, as described by Sevilla and Erdil, 2022, suggests that the chances of power-law scaling in compute ending in some important sense over the next 10 OoM is only 1 - (1 + 10/20)^(-1) = ⅓. Moreover, existing theoretical work provides compelling reasons for expecting this type of scaling relationship to continue (such as Sharma et al., 2022 and Bahri et al., 2021). ↩