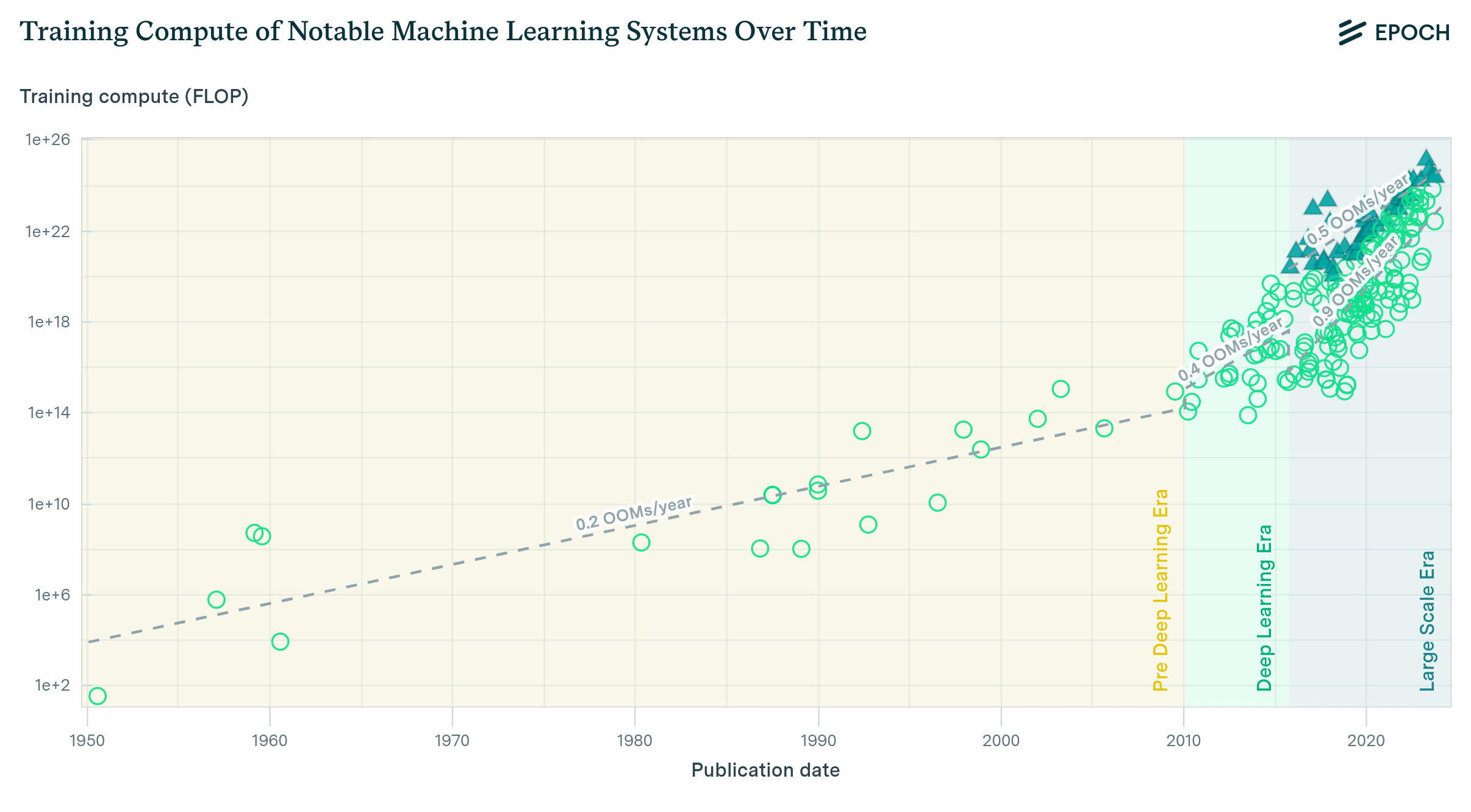
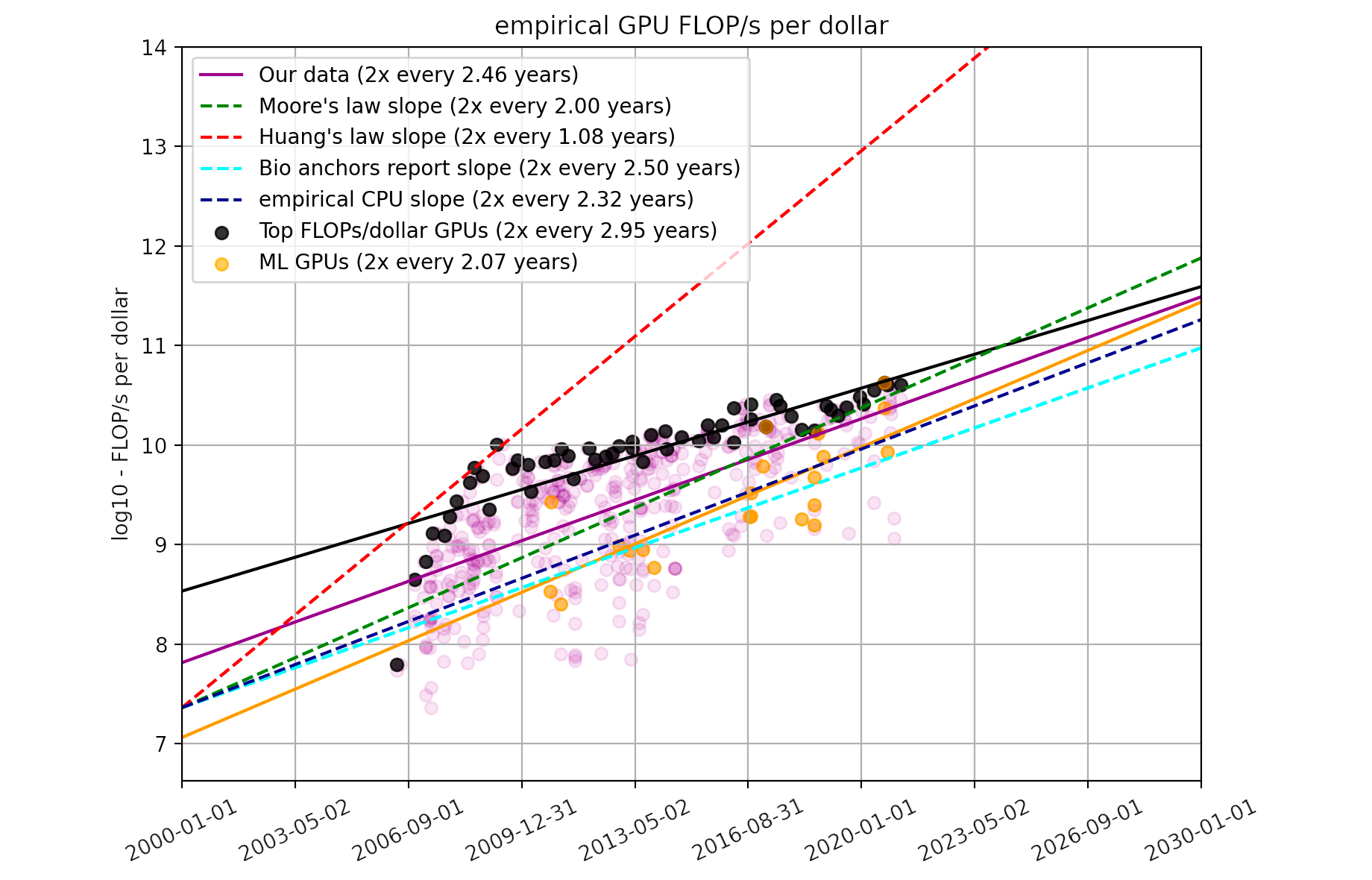
The Longest Training Run
Training runs of large machine learning systems are likely to last less than 14-15 months. This is because longer runs will be outcompeted by runs that start later and therefore use better hardware and better algorithms.
Published
Resources
In short: Training runs of large machine learning systems are likely to last less than 14-15 months. This is because longer runs will be outcompeted by runs that start later and therefore use better hardware and better algorithms.
[Edited 2023/06/28 to fix an error in the hardware improvements + rising investments + software improvements calculations. We thank Nick Gabrieli for noticing the mistake.]
[Edited 2022/09/22 to fix an error in the hardware improvements + rising investments calculation.]
| Scenario | Longest training run |
| Hardware improvements | 3.55 years |
| Hardware improvements + Software improvements | 1.22 years |
| Hardware improvements + Rising investments | 9.12 months |
| Hardware improvements + Rising investments + Software improvements | 6.49 months |
Larger compute budgets and a better understanding of how to effectively use compute (through, for example, using scaling laws) are two major driving forces of progress in recent machine learning.
There are many ways to increase your effective compute budget: better hardware, rising investments in AI R&D and improvements in algorithmic efficiency. In this article we investigate one often-overlooked but plausibly important factor: how long—in terms of wall-clock time—you are willing to train your model for.
Here we explore a simple mathematical framework for estimating the optimal duration of a training run. A researcher is tasked with training a model by some deadline, and must decide when to start their training run. The researcher is faced with a key problem: by delaying the training run, they can access better hardware, but by starting the training run soon, they can train the model for longer.
Using estimates of the relevant parameters, we calculate the optimal training duration. We then explore six additional considerations, related to 1) how dollar-budgets for compute rise over time, 2) the rate at which algorithmic efficiency improves, 3) whether developers can upgrade their software over time 4) what would happen in a more realistic framework with stochastic growth, 5) whether it matters for the framework that labs are not explicitly optimizing for optimal training runs and 6) what would happen if they rent instead of buy hardware.
Our conclusion depends on whether the researcher is able to upgrade their hardware stack while training. If they aren’t able to upgrade hardware, optimal training runs will likely last less than 3 months. If the researcher can upgrade their hardware stack during training, optimal training runs will last less than 1.2 years.
These numbers are likely to be overestimates, since 1) we use a conservative estimate of software progress, 2) real-world uncertainty pushes developers towards shorter training runs and 3) renting hardware creates an incentive to wait for longer and parallelize the run close to the deadline.
| Scenario | Longest training run |
| Hardware improvements | 3.55 years |
| Hardware improvements + Software improvements | 1.22 years |
| Hardware improvements + Rising investments | 9.12 months |
| Hardware improvements + Rising investments + Software improvements | 6.49 months |
A simple framework for training run lengths
Consider a researcher who wants to train a model by some deadline \(T\). The researcher is deciding when to start the training run in order to maximize the amount of compute per dollar.
The researcher is faced with a key trade-off. On one hand, they want to delay the run to access improved hardware (and/or other things like larger dollar-budgets and better algorithms.) On the other hand, a delay reduces the wall-clock time that the model is trained for.
Suppose that hardware price-performance is increasing as follows:
\[H(t) := H_0 \operatorname{Exp}[g_H t]\]
where \(H_0\) is the initial FLOP/$/time and \(g_H\) is the rate of yearly improvement1. If we start a training run at time \(S\), the cumulative FLOP/$ at time \(t\geq S\) will be equal to:
\[F_S(t) := H(S) (t-S)\]
where \(H(S)\) is the price-performance of the available hardware when we start our run (in FLOP/$/time), and \((t-S)\) is the amount of time since we started our run. Given a fixed dollar-budget, when should we buy our hardware and start a training run to achieve the most FLOP/$ by a deadline \(\)\(\)\(T\)?
To figure that out, we need to find the most efficient time \(\)\(S\) to start a run that concludes by time \(T>S\). We can find that by differentiating \(F_S(T)\) with respect to \(S\) and setting the result equal to zero.
\[\frac{\partial F_S(T)}{\partial S} = H(S) [g_H(T-S) - 1] = 0\]\[T-S = 1 / g_H\]
The optimal training run has length \(L := T-S = 1/g_H\). In previous work we estimate the rate of improvement of GPU cost effectiveness at \(g_H \approx 0.281\) (Hobbhahn and Besiroglu, 2022) 2. This leads to an optimal training run of length \(L = 1 / g_H \approx 3.55\) years.

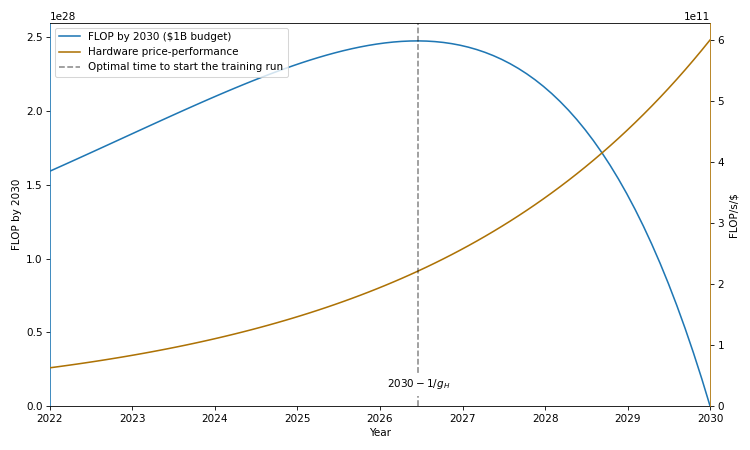
In blue, total amount of compute consumed by training runs starting at different years, given a deadline \(T = 2030\) and an investment of $1B. In brown, the hardware price-performance, assuming an initial price-performance of \(H_0 \approx ~6.3 \times 10^{10} \; \text{FLOP/s/\$}\) in 2022 and a rate of improvement of \(g_H \approx 0.281\) (see Hobbhahn and Besiroglu, 2022).
The intuition is as follows: if you want to train a model by a deadline \(T\), then, on the one hand, you want to wait as long as possible to get access to high price-performance hardware. On the other hand, by waiting, you reduce the total time available for your training run. The optimal training duration is the duration that strikes the right balance between these trade-offs.
This calculation rests on some assumptions:
- We are ignoring that willingness to invest in ML rises over time, so a researcher might be able to secure a larger budget if they wait
- We are ignoring that improvements in software and better understanding of scaling laws might enable researchers to deploy compute more effectively in the future
- We are assuming that practitioners will not upgrade their hardware in the middle of a run
- We are assuming that the involved quantities will improve at a predictable, deterministic rate
- We are assuming that developers optimize for a fixed deadline
- We are assuming that developers are buying their own hardware
Let’s relax each of these assumptions in turn and see where they take us.
Accounting for increasing dollar-budgets
In reality, the total amount of compute invested in ML training runs has grown faster than GPU price performance. Companies have been increasing their dollar-budgets for training ML models; hence, researchers might want to delay training ML models to access larger dollar-budgets.
Our previous work found a rate of growth of compute invested in training runs equal to \(g_C \approx 1.31\) 3. This rate of growth can be decomposed as \(g_C = g_H + g_I\), the sum of hardware efficiency growth \(g_H \approx 0.281\) and the growth in investment \(g_I = g_C - g_H \approx 1.03\) 4.
Following the same reasoning as above, we can calculate the optimal training run length equal to \(L = 1 / g_C \approx 0.76\) years, ie \(9.12\) months.
This is much shorter than the ~\(3.55\) year training duration we saw previously. Researchers want to wait for both better hardware and larger dollar-budgets. Since dollar-budgets have been growing about an order of magnitude more quickly than hardware price-performance has been improving, researchers taking into account growing dollar-budgets will train their models for roughly an order of magnitude less wall-clock time.
Accounting for increased algorithmic efficiency
In 2020, Kaplan et al´s paper about scaling laws for neural models provided practitioners with a recipe for training models in a way that leverages compute effectively. Two years after, Hoffman et al upended the situation by releasing an updated take on scaling laws that helped spend compute even more efficiently.
Our understanding of how to effectively train models seems to be rapidly evolving. Hence, practitioners today might be dissuaded from planning a multiyear training run because advances in the field might render their efforts obsolete.
One way we can study this phenomenon is by understanding how much less compute we need today to achieve the same results as a decade ago. While partially outdated in the light of new developments, Hernandez and Brown’s measurement of algorithmic efficiency remains the best work in the area.
They find a 44x improvement in algorithmic efficiency over 7 years, which translates to a rate of growth of \(g_S \approx 0.541\).
Combining this with the rate of improvement of hardware leads to a combined rate of growth of \(g_H + g_S \approx 0.281 + 0.541 = 0.822\). This translates to an optimal training run length of \(L = 1 / (g_H+g_S) \approx 1.22\) years.
We could also combine this with the rate of growth of investments. In that case we would end up with a total rate of growth of effective compute equal to \(g_H + g_I + g_S \approx 0.28 + 1.03 + 0.54 = 1.85\). This results in an optimal training run length of \(L = 1/(g_H + g_I + g_S) \approx 0.54\) years, ie \(6.49\) months.
Accounting for hardware swapping
Through this analysis we have assumed that ML practitioners commit to a fixed hardware infrastructure. However, in theory one could stop the current run, save the current state of the weights and the state of the optimizer, and resume the run in a new hardware setup.
Hypothetically, a researcher could upgrade their hardware as time goes on. In practice, if our budget is fixed this is a moot consideration. We want to spend our money at the point where we can buy the most compute per dollar before a deadline. Spending money before or afterwards leads to less returns per dollar overall.
Our budget does not need to be fixed however. As investments rise, we could use the incoming money buying new, better hardware to grow our hardware stock.
Suppose that the amount of available money at each point grows as \(g_I\). We can spend money at any time to buy state-of-the-art hardware, whose cost-efficiency has been improving all along at a pace \(g_H\).
\[H(t) := H_0 \operatorname{Exp}[g_H t]\]\[I(t) := I_0 \operatorname{Exp}[g_I t]\]
There are many possible ways to spend the budget over time. However, the optimal solution will be to spend all available budget at the point that maximizes the product between hardware cost-efficiency and time remaining, and then spend any incoming money afterwards as soon as possible to get higher returns.
Formally, the cumulative amount of FLOP that a run started at point \(S\) can muster by time \(t > S\) is equal to:
\[F_S(t) := \underbrace{H(S) I(S) (t-S)}_{\text{FLOP yield of initial hardware}} + \underbrace{\int_S^t H(u) \dot I(u) (t-u) du}_{\text{FLOP yield of hardware swapping}}\]
Differentiating with respect to \(S\) as before gives us the optimal training run length:
\[\frac{\partial F_S(T)}{\partial S} = H(S) I(S) [(g_H+g_I) (T-S) - 1] - H(S) I(S) g_I (T-S) = 0\]\[L := T-S = 1/g_H\]
The answer is the same as in the case where our budget is fixed, there are no rising investments and swapping hardware is not allowed. I.e., we find that the influence of the rising budget disappears - the optimal length of the training run now depends only on the rate of hardware improvement.
This is simply because there is no additional incentive to wait for larger dollar-budgets; researchers reap the benefits of growing hardware-budgets by default. Hence, the optimal duration of a training run is the same as that found when only considering hardware price-performance improvements.
Accounting for stochasticity
In our framework we have assumed a simple deterministic setup where hardware efficiency, investments and algorithmic efficiency rise smoothly and predictably.
In reality, progress is more stochastic. New hardware might overshoot (or undershoot) expectations. Market fluctuations and the interest in your research area may affect the dollar-budget you can muster for training at any given point.
Developing a framework that incorporates stochasticity is beyond the scope of this article. However, it may be useful to consider an idea from portfolio theory: when you’re not sure what will happen in the future, you don’t want to lock up capital in long-term projects. This pushes training runs towards being shorter—and means that the numbers we are estimating in this article are likely on the higher side.
Fixed deadlines
One possible objection to our framework is that it assumes developers are trying to hit a fixed deadline. In reality, researchers are often happy to wait for longer results.
Ultimately, we believe that this is a good framework. The way we conceptualize research in AI envisions many labs beginning their training runs at different times.
In any given quarter, the lab that releases the most compute-intensive model will be the one that started their training run closest to the optimal length.
Even if labs are not optimizing for explicit deadlines or planning training lengths, the most compute-efficient among them will still roughly obey these rules. Labs that train for shorter and longer times than the optimum will be outclassed.
Assuming that the most compute-intensive models will also be the most impressive, then this model provides a good upper bound on training lengths of impressive models.
Renting hardware
Through this discussion we have been assuming that labs purchase rather than rent hardware for training. This is the case for some of the top labs that usually train the largest models, such as Google and Meta. However, many others instead resort to renting hardware use from cloud computing platforms such as Amazon AWS, Lambda Labs or Google Cloud.
In the case hardware is rented, and there the training run require a small fraction of the available capacity, we expect our model not to apply. Since hardware prices decrease over time and training runs are largely paralellizable, there is a strong incentive for labs that rent hardware to wait for as long as possible, and train their model very briefly on a much larger number GPUs (relative to the number that is optimal when hardware is purchased) close to their deadline.
While we think this is an important case to consider (as renting hardware is likely much common in machine learning relative to using purchased hardware), since we’re mostly interested in understanding the decision-problems associated with training the largest models at any point in time, we have not studied the case of renting hardware in much depth.
Conclusion
We have analyzed how continuously improving hardware, bigger budgets and rising algorithmic efficiency limit the usefulness of a longer training run.
Researchers are faced with a trade-off when deciding when to start a training run that ends at some time \(T\). On one hand, they want to delay the start of this run to get access to improved hardware and/or additional factors like larger dollar-budgets and better algorithms. On the other hand, a delay reduces the time that the hardware can deployed for. Since we have some sense of the rate at which these factors change over time, we can infer the optimal duration of ML training runs.
We find that optimally balancing these trade-offs implies that the resulting training runs should last somewhere between 2.5 months and 3.6 years.
Allowing for swapping hardware removes the effect of rising budgets (since we can spend incoming money without stopping the run). This increases the optimal training run length to between 1.2 and 3.6 years.
We expect these numbers to be overestimates, since improvements are stochastic, uncertainty will push developers to avoid over-investing in single training runs, and renting hardware incentivizes developers to wait longer before starting their training run.
Furthermore, large-scale runs can be technically difficult to implement. Hardware breaks and needs to be replaced. Errors and bugs force one to discard halfway completed training runs. All these factors shorten the optimal training run5.
The biggest uncertainty in our model is the rate at which algorithmic efficiency improves. We have used an estimate from (Hernandez and Brown, 2020) to derive the result. This paper precedes the conversation about scaling laws and uses data from computer vision rather than language models. Our sense is that (some types of) algorithmic improvements have proven to be faster than estimated in that paper, and this could further shorten the optimal training run.
In any case, we can conclude that at current rate of hardware improvement we probably will not see runs of notable ML models over 4 years long, at least when researchers are optimizing compute per dollar.
| Scenario | Longest training run |
| Hardware improvements | 3.55 years |
| Hardware improvements + Software improvements | 1.22 years |
| Hardware improvements + Rising investments | 9.12 months |
| Hardware improvements + Rising investments + Software improvements | 6.49 months |
Acknowledgements
We thank Sam Ringer, Tom Davidson, Ben Cottier, Ege Erdil and Lennart Heim for discussion.
Thanks to Edu Roldan for preparing the graph in the post.
-
We assume that hardware price performance increases smoothly over time, rather than with discontinuous jumps corresponding to the release of new GPU designs or lithography techniques. We expect that on a more realistic step-function process, the key conclusions of our framework would still roughly follow (modulo optimal training durations occasionally changing a few months to accommodate discrete generations of hardware). ↩
-
They find a doubling time for hardware efficiency of 2.46 years. This corresponds to a yearly growth rate of \(g_H \approx \frac{\ln{2}}{2.46} = 0.281\). ↩
-
We found a 6.3 month doubling time for compute invested in large training runs. This is a yearly growth rate of \(g_C \approx \frac{\ln{2}}{6.3 \text{months} \cdot \frac{\text{year}}{12 \text{months}}} = 1.31\). ↩
-
In theory, we should also account for the rise in training lengths. In practice, when we looked at a few data-points training lengths appeared to be increasing linearly over time, so we believe the effect is quite small. ↩
-
Meta’s OPT logbook illustrates this well: they report being unable to continuously train their models for more than 1-2 days on a cluster of 128 nodes due to the many failures requiring manual detection and remediation. ↩