Limits to the Energy Efficiency of CMOS Microprocessors
How far can the energy efficiency of CMOS microprocessors be pushed before we hit physical limits? Using a simple model, we find that there is room for a further 50 to 1000x improvement in energy efficiency.
Published
Resources
Summary
Compared to the ENIAC in 1946, modern microprocessors can perform roughly a quadrillion times more computations for every unit of dissipated energy. This illustrates one of the most important trends in the history of computing – Koomey’s Law – under which the energy efficiency of computers has increased drastically over the last eight decades.
But how much longer can this progress persist before hitting physical limits? The answer to this question has important implications for forecasts of future progress in hardware: if we are close to the fundamental limits, the returns to hardware R&D within the existing paradigm of Complementary Metal-Oxide Semiconductor (CMOS) processors may rapidly diminish in the near future.
In our new paper, published in the IEEE International Conference on Rebooting Computing, we propose a simple model of energy efficiency to shed light on this question. This allows us to estimate an upper bound to the energy efficiency of CMOS microprocessors, measured in Floating Point Operations per Joule of dissipated energy (FLOP/J). Our work expands on previous analysis by analyzing the limits to dissipation in wire interconnects, and provides a more rigorous framework for forecasting energy efficiency limits, which accounts for uncertainty and can be iterated upon in future research.
Our core model considers two primary sources of energy dissipation, one from switching transistors in logic operations, and the other from data communication in wire interconnects:
\[E = E_\text{transistor} + E_\text{interconnect},\]where each of these terms describes the energy dissipated per FLOP. The contribution from transistor switches can be simply decomposed as a product of the energy per transistor switch \(Q_S\) and the number of transistor switches per FLOP \(N_T\).
\[E_\text{transistor} = Q_S \times N_T\]The \(E_\text{interconnect}\) contribution is determined by the geometry of CMOS microprocessors. In particular, wire interconnects are typically surrounded by other wires as well as a metal substrate, which results in a measurable capacitance \(C\) that gets charged and discharged when communicating information. Given an exogenous supply voltage \(V\), this results in an energy cost \(CV^2\), where we drop a factor of half to account for both charging and discharging capacitances. We estimate \(C\) by splitting it into the product of the capacitance per unit length \(C_L\), the average length of a charged wire \(L\), and the number of charged wires per FLOP \(N\), which yields
\[E_\text{interconnect} = C_L \times L \times N \times V^2.\]Our core parameter estimates are summarized in the table below, and the parameter estimates are described in detail in the full paper:
| Variable | Range |
|---|---|
| Energy per switch \(Q_S\) | \([3 \times 10^{-20}, 10^{-18}]\) J/switch |
| Number of switches \(N_T\) | \([30, 3000]\) switches |
| \(1/E_\text{transistor}\) | \([3.3 \times 10^{14}, 1.1 \times 10^{18}]\) FLOP/J |
| Capacitance per unit length \(C_L\) | \([2 \times 10^{-11}, 2 \times 10^{-10}]\) F/m |
| Avg. wire length \(L\) | \([12.5 \times 10^{-9}, 190 \times 10^{-9}]\) m |
| Number of wires \(N\) | \([30, 3000]\) wires |
| Supply voltage \(V\) | \([0.1, 0.6]\) V |
| \(1/E_\text{interconnect}\) | \([1.5 \times 10^{13}, 1.3 \times 10^{18}]\) FLOP/J |
Summary of all upper and lower bounds for the key variables in the model.
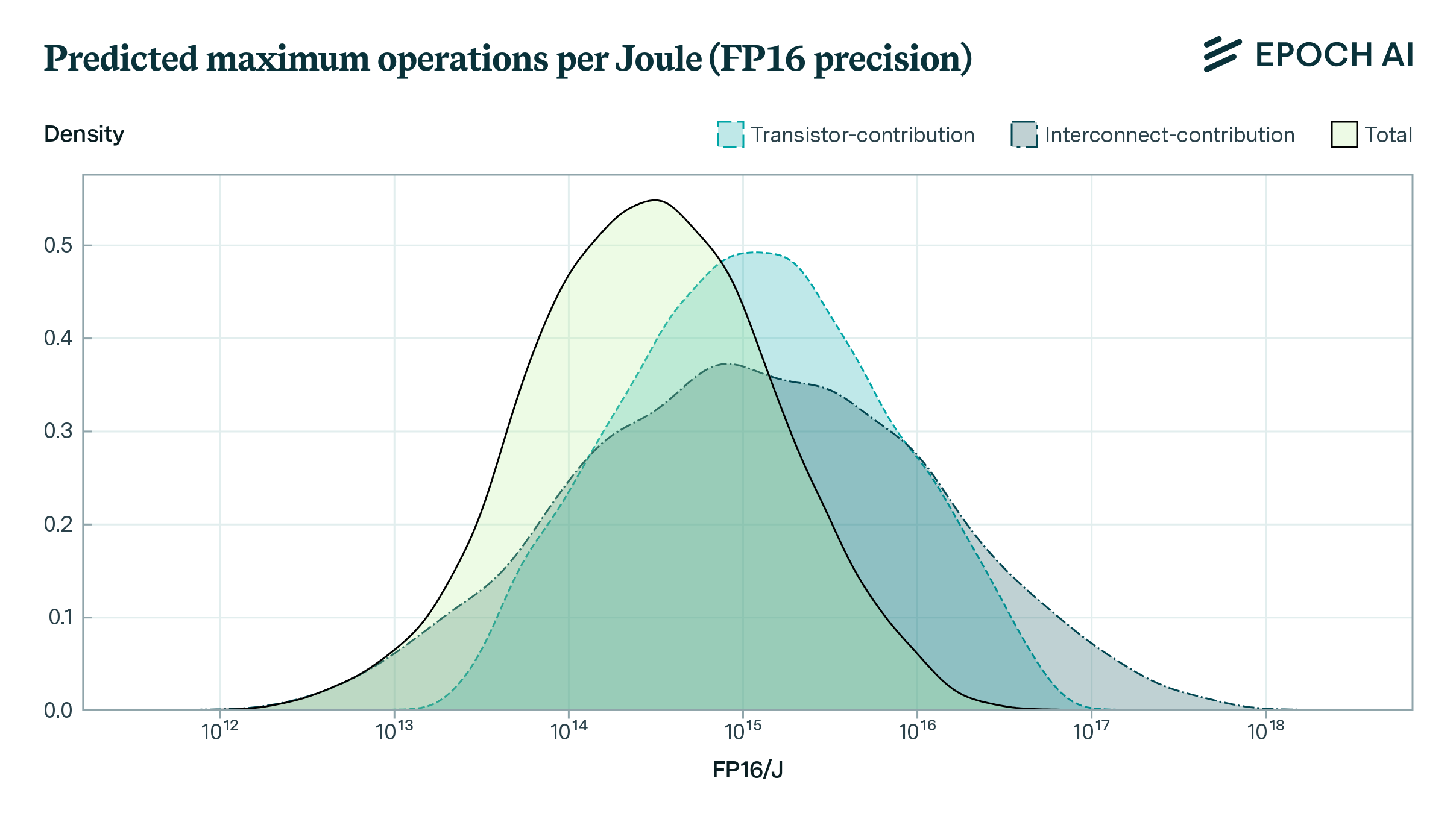
Given these ranges, we determine a distribution over the predicted FLOP/J using Monte Carlo simulation. This has a geometric mean of around \(5 \times 10^{15}\) FLOP/J at 4-bit precision, with a log-space standard deviation of 0.7 orders of magnitude. If we assume that the energy cost scales quadratically with the number precision, we end up with a geometric mean of \(2.9 \times 10^{14}\) FLOP/J at 16-bit precision.
In conclusion, we have proposed a simple model for estimating the physical limits to the energy efficiency of CMOS microprocessors, which accounts for energy costs from transistor switching and interconnects. Our work should be seen as a first-pass at estimating the limits to the FLOP/J that further work can improve upon, such as by synthesizing a more detailed understanding of wire interconnects, the feasibility of voltage scaling, and the importance of static power dissipation.
Implications
The H100 GPU has an energy efficiency of around \(1.4 \times 10^{12}\) FLOP/J. Our results for 16-bit precision operations therefore suggest that there is a 50% chance that further improvements will cease before a roughly \(200 \times\) improvement on existing technology.
These days, energy costs make up only a small fraction of the cost of computation. However, while the cost of computation is dropping rapidly, our FLOP/J bound could set upper limits on the feasibility of computationally-intensive tasks.
For instance, one question we could ask is this: how large would a training run need to be, in order for the associated annual energy costs to be intolerably large? We can give a rough answer to this question by splitting this maximum FLOP/year into two parts:
\[\text{FLOP/year} = \text{FLOP/J} \times \text{J/year}.\]If we assume that a year-long training run has a maximum energy availability equivalent to that of 2021 global primary energy consumption, then the maximum tolerable energy cost is 5e20 J/year. Combining this with our median FLOP/J estimate yields an upper bound of around 1e35 FLOP/year using 16-bit operations. This is roughly 10-billion-fold more computation than was used to train GPT-4!
Our estimates therefore suggest that CMOS processors are likely sufficiently efficient to power substantially larger AI training runs than today, if annual energy costs are the only consideration. Of course, in practice there are various other considerations that ought to be considered, such as financial viability of extremely large training runs, difficulties with scaling compute clusters, etc. Training runs beyond 1e35 physical FLOP would likely require radical changes, such as through a shift to adiabatic computing.