Introduction

Reusing pre-trained models often saves training costs. In the current large-scale paradigm, foundation models are routinely re-used by fine-tuning a general foundation model on specific tasks (Bommasani et al. 2022). But it is also possible to save costs by re-using an older foundation model to train a newer foundation model. Let’s call this practice “foundation model recycling”, which can be distinguished from the more general phenomenon of model re-use (Jiang et al. 2023). This short report investigates the benefits and implications of recycling foundation models.

There appear to be two general ways of recycling foundation models. The first method is by employing a student-teacher setup with the older model as a teacher for at least some time during training. In deep reinforcement learning, this method is generally known as kickstarting, and helps cut down on training costs by providing a dense reward signal during the early stages of training (Schmitt et al. 2018). The second method is to augment the older model with a modified architecture or learning algorithm, possibly making it larger and training it for longer or on different data. This could involve, for example, pruning the old model and using the pruned model as one component in the new model (e.g. Qi et al. 2023).

If model recycling is generally useful and becomes widely adopted as a result, we can anticipate some major consequences:

• a general increase in the performance for SOTA (state of the art) models. Training compute expended on earlier models can partially substitute for the compute needed in subsequent training runs.

• early models that are repeatedly recycled may influence the properties of later SOTA models. If this happens, current development might have greater leverage over the properties of future models than we might have otherwise thought, which may be an important consideration for AI safety.

• it may become harder to train SOTA models unless one has access to the previous SOTA models.

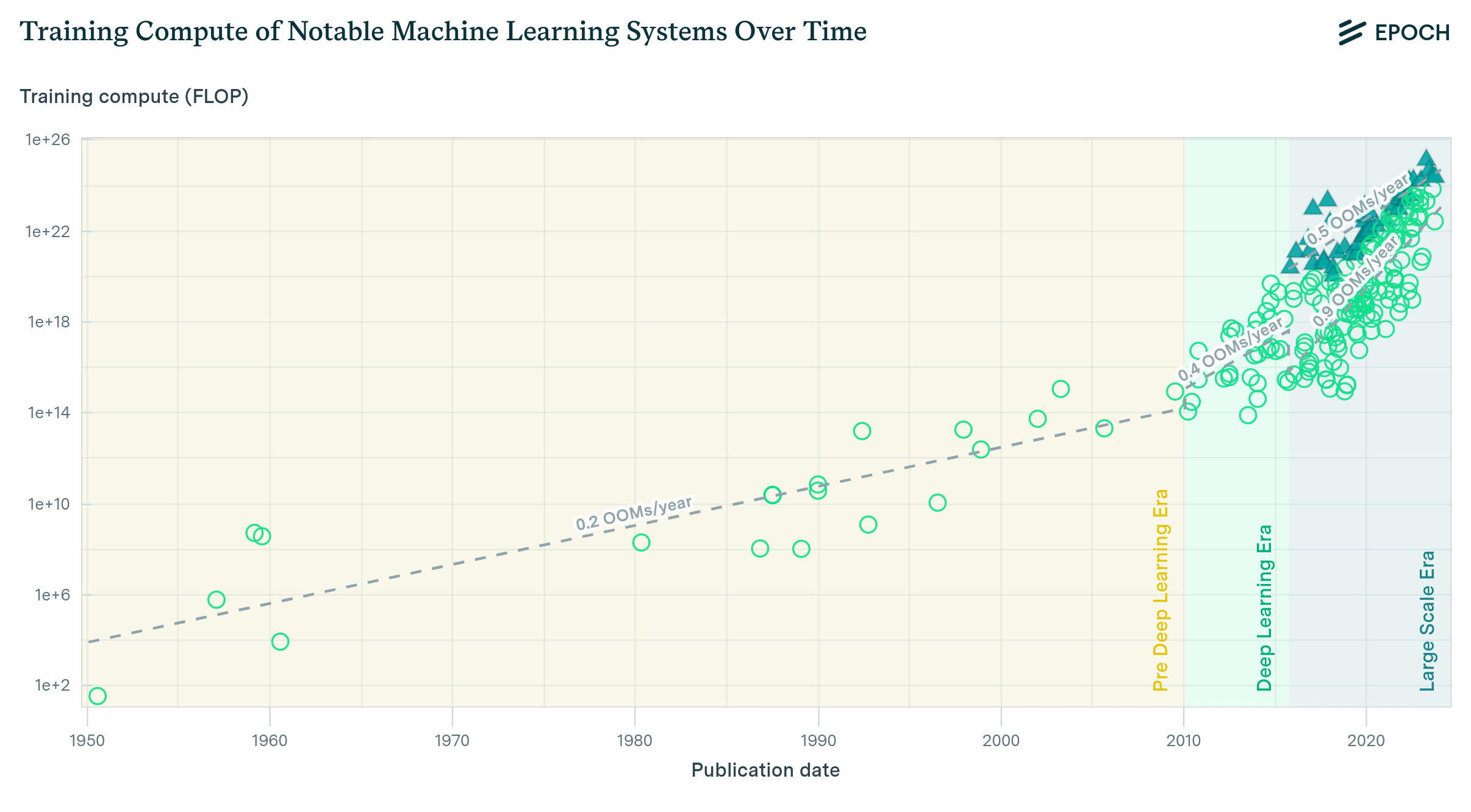
In this report, I study the benefit of model recycling. The primary result is that the benefits of model recycling are small. Although the benefits of model recycling add up over time, the effect is linear and thus only provides a minor benefit compared to the exponential growth in compute budgets and algorithmic progress that we’ve observed historically.

More specifically, if compute budgets (in FLOP) increase by a factor of \(r\) each year, then the ratio of physical compute available in year \(T\) to the sum of compute over all years is given by \(\frac{C_0 r^T}{\sum_{t=0}^T C_0 r^t} =\frac{r-1}{r^{T+1}-1} \cdot r^T\). For large \(T\), this ratio approaches \((r-1)/r\), which is close to \(1\) for realistic values of \(r\), see Table 1.

Considered growth rate	Growth rate	Recycling advantage
Current compute increase	4.2x/year	1.3x
Hardware efficiency	1.3x/year	4.1x
Current compute increase + Software efficiency	10.5x/year	1.1x
Hardware efficiency + Software efficiency	3.3x/year	1.4x

Table 1: Maximum compute multiplier for various growth rates of the effective compute budget used to train foundation models. We consider current physical compute growth rates, the growth rates at a fixed level of investment and the effect of algorithmic progress in both situations. We have taken the growth rates from Epoch AI 2022. The compute multiplier is the effective multiple on compute for a training run as a result of model recycling, or in other words, the multiple of compute required to obtain the same performance without recycling.

In fact, there may be no benefit at all from augmenting old models with new algorithms if inefficiencies in the older models deteriorate future performance. This result is plausible because model augmentation implicitly recycles old architectures, which may learn more slowly than newer architectures, decreasing our ability to take advantage of algorithmic progress. Both of these approaches will be considered in more detail in the rest of this report.

Modeling model recycling

As explained previously, we can distinguish between two forms of model recycling.

1. Kickstarting, in which a student model learns from the outputs of an older teacher model. This technique is generally beneficial because it provides a high-quality, dense reward signal during the initial stages of training (Schmitt et al. 2018).

2. Model augmentation, in which an older model is augmented with new algorithms, such as a newer optimizer, or an additional recurrent layer, and trained for longer or with different data (e.g. Qi et al. 2023).

These approaches differ by what is being recycled. In the first approach, knowledge is recycled and distilled into the new model; in the second approach, the model weights themselves are recycled.

Both approaches promise some efficiency benefits when performed over few iterations. However, since model augmentation involves recycling model weights, it also carries the risk of deteriorating performance. The reason is that recycling model weights implicitly recycles old architectures, which may learn more slowly than newer architectures. As a consequence, it appears that kickstarting, rather than model augmentation, will be more beneficial, especially over long sequences in which models are repeatedly recycled. At the same time, kickstarting comes with its own defects. Since kickstarting requires re-learning what was already known, it is more wasteful than model augmentation. These costs and benefits are worth considering in detail.

In each case, we assume that the goal of model recycling is to increase adjusted compute, defined as the hypothetical amount of compute that would be required to train a model from scratch to reach the same level of performance that the actual model reached during training while employing model recycling. The value of model recycling is measured by the ratio of adjusted compute to real compute \(A/C\), which is beneficial when \(A/C > 1\).

Kickstarting

At the core of kickstarting is the idea of training a new model using the outputs of a previous model, so that it can more quickly reach a baseline level of performance than if it trained from scratch. The rate at which it can reach this baseline level of performance determines the benefits. In the original paper on kickstarting, it was claimed that kickstarting can help the new model learn to a baseline level in as few as 10 percent the number of total training steps compared to learning from scratch (Schmitt et al. 2018).

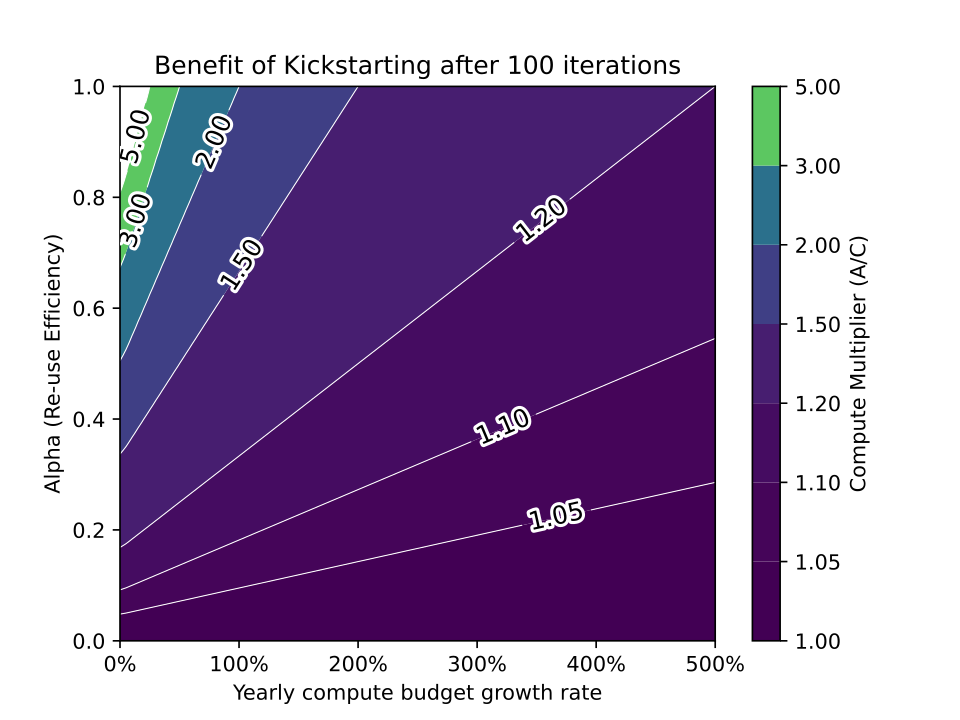
Let’s sketch a model of model recycling using kickstarting. During the first training iteration, a model is trained from scratch with adjusted compute equal to real compute \(C_1 = A_1\). During each subsequent iteration (which will happen once per year), the real compute budget will grow at a constant rate \(r\). The amount of adjusted compute during each subsequent iteration is equal to the real compute allocated for that run, plus the amount of adjusted compute during the previous training run multiplied by a re-use efficiency parameter \(0 \leq \alpha \leq 1\). In summary, \(C_n = rC_{n - 1}, n > 1\) \(A_1 = C_1\) \(A_n = C_n + \alpha A_{n - 1}\) The starting compute \(C_1\) does not affect the benefit of model recycling in this model. Instead the benefit is determined solely by \(r\) and \(\alpha\). The benefit, as measured by \(A/C\), is plotted below after effectively infinite iterations (years) in Figure 1.

Figure 1: The benefit of kickstarting, as measured by the ratio of adjusted compute to real compute after effectively infinite iterations under various possible settings of the rate of growth of compute budgets \(r\) and the re-use efficiency \(\alpha\).

The benefit is increased after each iteration. However, this sequence quickly converges for most choices of \(r\) and \(\alpha\), as illustrated in Figure 2.

Figure 2: The benefit of kickstarting after repeated variations under various possible settings of the rate of growth of compute budgets \(r\) and the re-use efficiency \(\alpha\).

So far, this model has not accounted for algorithmic progress, which can only yield more modest results. Algorithmic progress refers to the trend of algorithms requiring less compute or data to reach the same level of performance as previous algorithms. There seem to be two ways of incorporating algorithmic progress in this model: we can either (1) decrease our estimate of the re-use efficiency, \(\alpha\), as a result of better algorithms requiring less time to reach the same baseline level of performance compared to older algorithms, or (2) replace real compute with effective compute, which is adjusted for algorithmic progress and grows faster as a result. In either case, we can re-use the results obtained in Figure 1 and Figure 2, while keeping in mind an adjustment for algorithmic efficiency.

For example, Erdil and Besiroglu 2023 estimated that algorithmic progress increases effective compute in computer vision at a rate of roughly 150% per year. Sevilla et al. 2022 estimated that the current trend for the compute for the largest training runs to grow at a rate of 130% per year. Combining these together yields a rate of growth of effective compute of 475% per year. It is easy to see that at such an extreme rate of growth, it is impossible for the benefit ratio to exceed even 1.5, which is a modest benefit considering the fact that training runs have historically grown by orders of magnitude over just a few years. This pessimistic conclusion is even stronger in the case of model augmentation.

Figure 3: The contribution to adjusted compute from kickstarting for values of \(\alpha=0.9\) and a rate of increase in effective compute of \(380\%\), where each year is one iteration.

Model augmentation

The central idea of model augmentation is that the model weights are re-used to train a new model rather than purely extracting knowledge from the previous model. However, since model weights intrinsically depend on the architectural details of a model for example, if one was re-using the weights for a convolutional layer model augmentation implicitly recycles old algorithms.

Some architectural algorithms have been found to be better at learning certain tasks. For instance, it has been found that self-attention is better suited for language prediction tasks compared to convolutional networks, at least above a certain scale (Tay et al. 2022). Re-using older, less efficient algorithms will therefore have the effect of deteriorating performance, which compounds over time as algorithmic progress continues.

To model the process of model augmentation, let’s assume that re-using model weights only lets us take partial advantage of algorithmic progress \(P\), which acts as a multiplier on real compute and grows exogenously at rate \(g\) as a result of machine learning research. The parameter \(\beta\) determines the fraction of new algorithmic progress that we can take advantage of during each iteration \(i\). We set up the model according to the following equations.

Just as before, we assume that compute grows exogenously at some rate \(r\). \(C_n = rC_{n - 1}, n > 1\) And we assume that the adjusted compute starts at the level of the training compute during the first iteration. \(A_1 = C_1\) However, this time we include a parameter that sets algorithmic efficiency, which grows at rate \(g\). \(P_1 = 1\) \(P_n = gP_{n - 1}\) The adjusted compute during each iteration is equal to the real compute during that iteration multiplied by the algorithmic efficiency times \(\beta\), plus the adjusted compute from the last iteration. \(A_n = \beta P_n C_n + A_{n-1}\) This last equation implies that the adjusted compute could grow more slowly than effective compute, or \(P_n C_n\). In this case, it is often preferable to train from scratch since the decrease in performance from values of \(\beta < 1\) ends up deteriorating performance for even relatively small values of \(n\). Some simulations of model augmentation under various parameter settings are shown in Figure 4. In fact, unless the re-use efficiency \(\beta\) is very close to \(1\) or the number of iterations is very small, the benefits to model augmentation appear modest or counterproductive in almost all cases. For this reason, it seems reasonable to expect that people will not employ model augmentation for more than a few iterations, if at all.

a)

b)

c)

d)

Discussion

In light of the modest benefits of both kickstarting and model augmentation, it seems likely that neither approach will increase the efficiency of large training runs for future large foundation models by more than a small degree. As a result, none of the anticipated effects of model recycling should be large either. To the extent that model recycling will still be employed, kickstarting appears more likely to be adopted compared to model augmentation, given that it permits researchers to upgrade algorithms while re-using knowledge obtained by models from prior training runs.

Nonetheless, one consideration that these simple models do not take into account is the degree to which algorithmic progress is endogenous, or caused by the scale-up of models themselves. Algorithmic progress could be endogenous if ML models themselves play a role in AI research, which may already be happening to a limited degree from limited AI tools like GitHub Copilot (Morris 2023). If performance via model recycling accelerates algorithmic progress, then the performance-enhancing effect of model recycling could be stronger than this simple analysis shows. It is an open question whether endogenizing algorithmic progress in these models significantly changes the overall conclusion that model recycling will have modest effects, or whether the pessimistic conclusion remains.

Future research could also focus on creating more realistic models by estimating the re-use efficiency parameter more accurately, and providing better estimates of the rate of algorithmic progress. It is possible that re-use efficiency depends on factors such as model scale and algorithmic progress, and therefore may not be constant over time, as was assumed in this analysis. Alternative methods of recycling foundation models may also be identified that do not neatly fall into the two categories of kickstarting or model augmentation. Finally, this report focuses almost exclusively on model recycling from a theoretical perspective; the details for how to best recycle foundation models is a topic for future research.

Acknowledgements

I want to thank Jaime Sevilla, Tamay Besiroglu, Pablo Villalobos, Tom Davidson, and Ben Cottier for helpful comments on this report.

References

Bommasani, Rishi et al. (2022). On the Opportunities and Risks of Foundation Models. arXiv: 2108.07258 [cs.LG].

Epoch AI (2022). Parameter, Compute and Data Trends in Machine Learning. Accessed: 2023-6-5. url: https://epochai.org/data/visualization.

Erdil, Ege and Tamay Besiroglu (2023). Algorithmic progress in computer vision. arXiv: 2212.05153 [cs.CV].

Jiang, Wenxin et al. (2023). An Empirical Study of Pre-Trained Model Reuse in the Hugging Face Deep Learning Model Registry. arXiv: 2303.02552 [cs.SE].

Morris, Meredith Ringel (2023). Scientists’ Perspectives on the Potential for Generative AI in their Fields. arXiv: 2304.01420 [cs.CY].

Qi, Binhang et al. (2023). Reusing Deep Neural Network Models through Model Re-engineering. arXiv: 2304.00245 [cs.SE].

Schmitt, Simon et al. (2018). Kickstarting Deep Reinforcement Learning. arXiv: 1803.03835 [cs.LG].

Sevilla, Jaime et al. (2022). Compute Trends Across Three Eras of Machine Learning. arXiv: 2202.05924 [cs.LG].

Tay, Yi et al. (2022). Scaling Laws vs Model Architectures: How does Inductive Bias Influence Scaling? arXiv: 2207.10551 [cs.LG].