Data movement bottlenecks to large-scale model training: Scaling past 1e28 FLOP
Data movement bottlenecks limit LLM scaling beyond 2e28 FLOP, with a "latency wall" at 2e31 FLOP. We may hit these in ~3 years. Aggressive batch size scaling could potentially overcome these limits.
Published
Resources
Introduction
Over the past five years, the performance of large language models (LLMs) has improved dramatically, driven largely by rapid scaling in training compute budgets to handle larger models and training datasets. Our own estimates suggest that the training compute used by frontier AI models has grown by 4-5 times every year from 2010 to 2024. This rapid pace of scaling far outpaces Moore’s law, and sustaining it has required scaling along three dimensions: First, making training runs last longer; second, increasing the number of GPUs participating in each training run; and third, utilizing more performant GPUs.
It’s relatively easy to scale the duration that a GPU cluster is used to train a model.1 However, in practice training runs rarely exceed 6 months. This is because both the hardware and software used for a training run risks becoming obsolete at timescales longer than this, and no lab would want to release a model which has become outdated immediately upon release. This sets a practical limit on how long training runs can become.
The alternative is to scale the size of training clusters, and this has been the primary way in which training compute scaling has been achieved. As an example, the original Transformer from Vaswani et al. (2017) was trained on 8 GPUs for 12 hours, while Llama 3.1 405B was trained on around 16,000 GPUs for around 2 months.
Scaling the sizes of training clusters, however, is not as easy as scaling the length of training runs: there are fundamental constraints arising from data movement to how many GPUs can effectively participate in a training run of bounded duration. The more GPUs participate in a single training run, all else equal, the more data has to be moved around per second both inside each individual GPU and also across different GPUs.
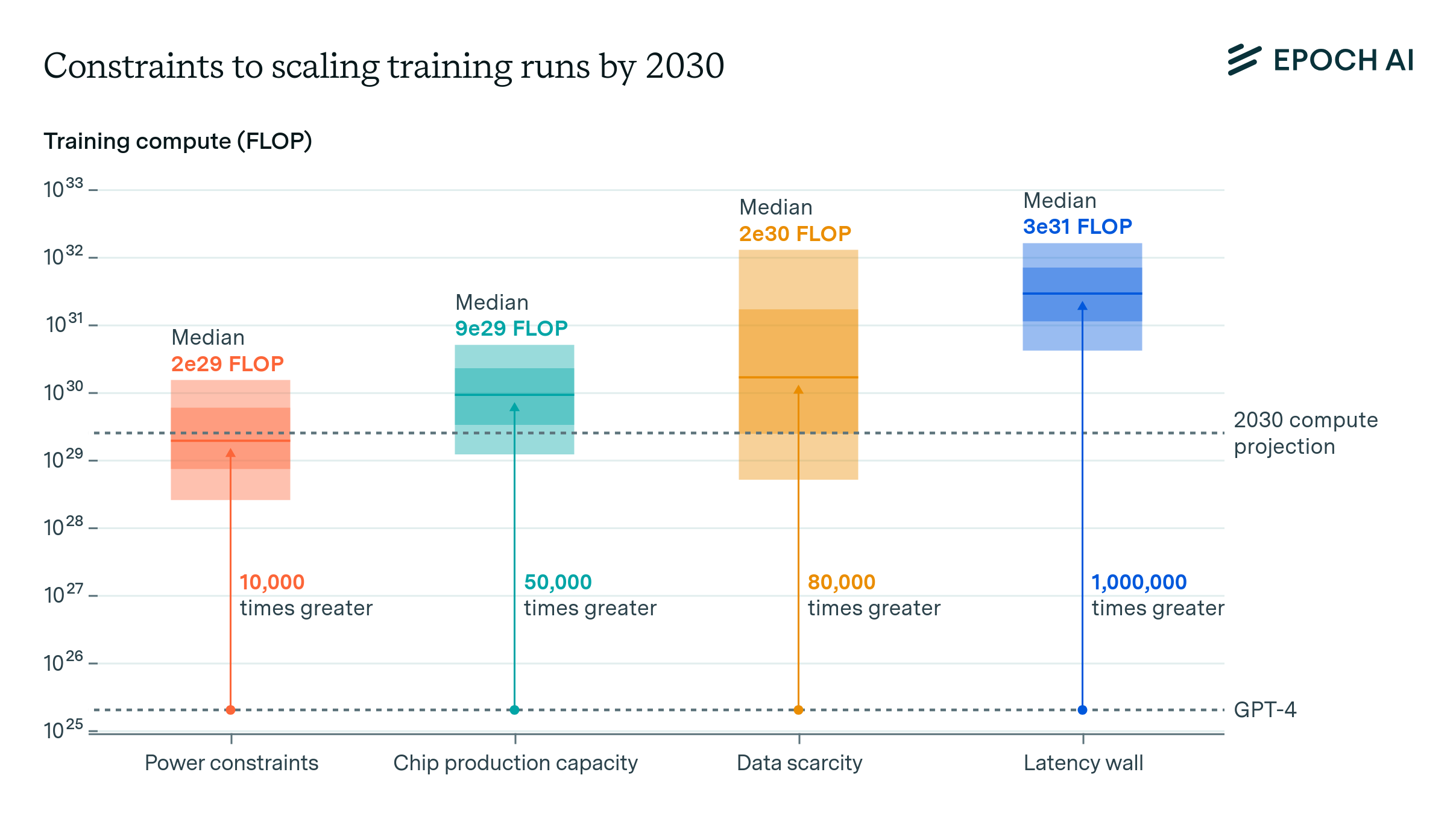
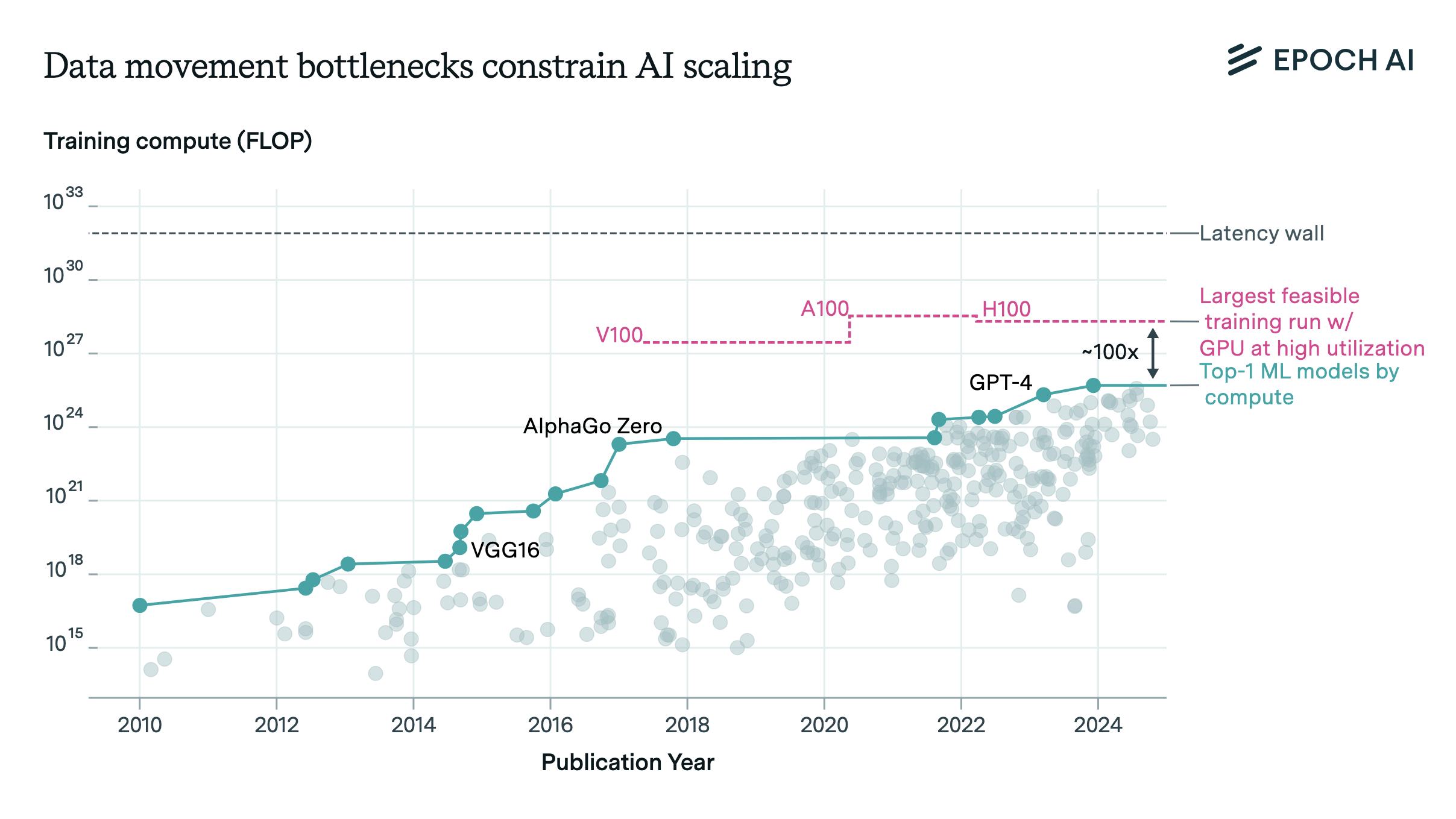
In a recent paper by Epoch AI researcher Ege Erdil and collaborator David Schneider-Joseph, we analyze the point at which data movement bottlenecks are likely to preclude further scaling of training runs with present technology. According to the estimates in our paper, if we assume a maximum duration of 3 months, training runs past a scale of \(2e28 \text{ FLOP}\) are infeasible to do efficiently. This is because past this training compute scale the time taken for data movement begins to dominate the time taken for arithmetic and it becomes impossible to make efficient use of hardware.
Figure 1. Training compute for top ML models is nearing the limits of current GPU technology, with data movement bottlenecks presenting a challenge. Current training runs are about 100x away from the limit beyond which scaling will face substantially reduced utilization. (Note that despite the H100’s higher arithmetic throughput, its maximum efficient training scale is actually lower than the A100’s due to interconnect and memory bandwidth not keeping pace with the arithmetic throughput, creating a more severe data movement bottleneck.)
If we disregard the degrading efficiency and try to scale clusters further at great expense, at some point we hit limits arising from network latency that set an upper bound on how quickly two devices in the cluster can talk to each other. Without fundamental technological improvements to interconnects, or switching from stochastic gradient descent variants to cheaper optimizers, it’s not possible to overcome these limits.
In this article, we will explore the data movement patterns during distributed training and analyze the limits to scaling large language models. We’ll examine both intra-GPU and inter-GPU data movement, discuss various parallelism methods, and investigate the constraints that arise as we push towards larger training runs. By the end, you will understand the challenges facing future scaling efforts, including utilization efficiency declines and the latency wall, as well as potential approaches to overcome these limitations.
Data movement patterns during distributed training
Before we can understand how data movement constrains distributed training, we need to cover the primary kinds of data movement that distributed training entails. Broadly, we can split these into two categories: intra-GPU data movement and inter-GPU data movement. We’ll cover each of these in turn.
Intra-GPU data movement
For current distributed training runs, high-bandwidth memory (HBM), also sometimes called VRAM, makes up almost all of the intra-GPU data movement cost. Essentially, if we wish to multiply two large matrices together, we need to read both matrices from HBM and then write the result back to HBM, and because memory bandwidth is not unlimited this takes a certain amount of time.
When the matrices involved in this operation are large (e.g. bigger than 10 million entries in total), the intra-GPU data movement costs are negligible because the arithmetic taking place in the cores of the GPU takes significantly longer than the memory reads. Using good kernel programming, it’s even possible to overlap most of the memory reads with ongoing arithmetic, and thus “hide” the memory reads behind arithmetic. However, as we scale down the size of our matrices, arithmetic time falls faster than memory read & write time2, and past some scale memory reads & writes become the bottleneck. At this scale, it becomes impossible to hide them and our arithmetic utilization starts to fall.
This imposes a constraint on distributed training for the following reason: according to the Chinchilla scaling law from Hoffmann et al. (2022), compute-optimal training requires scaling the training compute of a model quadratically with its number of parameters. However, the amount of arithmetic required for each Transformer block on a single batch typically scales roughly linearly with the number of parameters, depending on what we assume about how batch sizes can be scaled up with model sizes. This scaling discrepancy means the matrix multiplications in larger training runs need to be sliced into smaller pieces, and when these pieces are small enough along one of the three dimensions of a matrix multiplication, the memory bandwidth constraints might become binding.
Inter-GPU data movement
Inter-GPU data movement is necessary for the different GPUs to share results about their computations so that all of them can synchronously work on the same training run. There are four primary ways in which a training run can be parallelized, each requiring its own communication pattern between the participating GPUs. We list them below:
-
Data parallelism: Different GPUs process different input sequences or different tokens in a given batch. Each GPU can execute its forward and backward pass independently of the others, but before the weight update it’s necessary for them to share gradient information with each other. This requires communication to occur once before each gradient step.
-
Pipeline parallelism: Different GPUs handle different sequential blocks, or layers, of a Transformer. The output of one GPU is fed to the next as an input sequentially until an input makes it through all of the blocks of the model. This requires communication at each pipeline stage boundary. In addition, because of the sequential nature of the computation, doing this naively on a single batch leads to all GPUs except the currently active one being idle: this is called a pipeline bubble. Avoiding pipeline bubbles requires slicing the batch into micro-batches which are fed into the pipeline sequentially.
-
Tensor parallelism: Different GPUs handle the matrix multiplications by different parts of the model’s weight matrices: unlike pipeline parallelism which slices a model horizontally, tensor parallelism slices it vertically. The nature of tensor parallelism means that after every one or two matrix multiplications (depending on the exact implementation) the GPUs need to synchronize results with each other. This means tensor parallelism requires the most frequent communication between GPUs out of all parallelism methods, and as a result is currently only done over high-bandwidth and low-latency interconnects such as NVIDIA’s NVLink.
-
Expert parallelism: This type of parallelism only applies to models that have a mixture-of-experts (MoE) architecture. In these, each block is made up of many different “experts”, with different experts assigned to different GPUs. A cheap routing mechanism decides which experts each input will be sent to in each block. Once each activated expert finishes its computation, the results are merged before being sent to the next layer. As a result, expert parallelism requires communication in each block for expert routing and also for merging results from different experts.
Minimizing inter-GPU data movement for a fixed cluster size requires making use of multiple parallelism methods at once: this is because the data movement cost of each method scales linearly (or possibly sublinearly, in the case of tensor parallelism) with its parallelism degree, while the cluster size scales with the product of all parallelism degrees. Under these conditions, scaling all parallelism methods together minimizes the total data movement required for a given training run. As an example of what such a policy looks like in practice, the training run for Falcon-180B used 64-way data, 8-way pipeline and 8-way tensor parallelism in a cluster consisting of \(64 \cdot 8 \cdot 8 = 4096 \text{ GPUs}\).
The limits to scaling
When we take all of the above factors into account in a detailed model, we find that training runs beyond a scale of \(2e28 \text{ FLOP}\) (or, for compute-optimal dense models, around 15 trillion parameters) in the span of 3 months are infeasible to do with good utilization using current techniques and hardware. In addition, training runs past a scale of \(2e31 \text{ FLOP}\) are impossible due to latency constraints, at least if we do not compromise the logical integrity of stochastic gradient descent.
Figure 2: The predictions of our model about the best possible model FLOP utilization rate (MFU) that could be achieved for dense training runs at a given training compute scale.
Out of the factors constraining distributed training, the easiest to understand quantitatively is the latency wall, which sets an upper bound on which training runs can be completed within a fixed time window irrespective of how many GPUs are used. The basic reason behind the latency wall is that a bigger model typically requires more gradient steps during training, and if these have to be done in a fixed time window, this means each gradient step must take a shorter time as we scale the models we’re training. If this goes on long enough, eventually the time per gradient step becomes so short that latency constraints do not permit models of that size to be trained.
Understanding the latency wall
Quantitatively, say that our model has \(N\) parameters and is trained on \(D = 20N\) tokens according to the Chinchilla scaling law. With a batch size of \(B\) tokens, we will take \(n_{\text{steps}} = \frac{D}{B} = \frac{20N}{B}\) gradient steps during training, assuming a single epoch. If the time taken for our training run is \(t_{\text{train}}\), then each gradient step can take at most \(\frac{t_{\text{train}} \cdot B}{20 \cdot N}\) time.
On the other hand, if our training run is tensor-parallel at a high enough degree, we expect inter-GPU communication after each matrix multiplication, and depending on network latency each of these will take at least some time \(t_{\text{latency}}\)3. With e.g. 2 matrix multiplications per Transformer block and \(n_{\text{layer}}\) blocks in a Transformer, and the need to do one forward and one backward pass for each gradient step, the condition for a training run to be feasible under latency constraints becomes
\[4 \cdot n_{\text{layer}} \cdot t_{\text{latency}} \leq \frac{t_{\text{train}} \cdot B}{20 \cdot N}\] \[N \leq \frac{t_{\text{train}} \cdot B}{80 \cdot n_{\text{layer}} \cdot t_{\text{latency}}}\]Plugging in reasonable values such as \(t_{\text{latency}} = 9\) microseconds, \(n_{\text{layer}} = 120\), \(B = 4\) million tokens (used both during the training of GPT-3 and the training of Falcon-180B) and \(t_{\text{train}} = 3\) months gives \(N = 400\) trillion parameters, or if translated into the Chinchilla optimal training compute, around \(2e31 \text{ FLOP}\).
In practice, the number of layers \(n_{\text{layer}}\) and the batch size \(B\) are not constant but increase as models are scaled up. However, as long as the scaling of these two quantities roughly cancels out (which we believe might be the case) the calculation above is still going to hold. The more complex case where these two effects do not cancel is worked out in our paper, and we omit that calculation here in the interest of brevity.
We expect the latency wall to be the most challenging constraint to overcome in the future among the constraints discussed above, even though for current training runs latency is a negligible factor. There are two reasons for this:
-
Unlike memory bandwidth and network bandwidth limits, which we can scale past at the expense of getting worse utilization during training, the latency wall imposes an upper bound on model training compute (at fixed training time) that cannot be surpassed.
-
Out of all relevant hardware performance measures (such as HBM bandwidth, L2 cache bandwidth, network bandwidth…) the one that has improved slowest since the release of the V100 in 2017 is latency, both intra-device (such as kernel setup and tear down latencies) and inter-device (such as NVLink and InfiniBand latencies).
Possible ways to overcome the limits
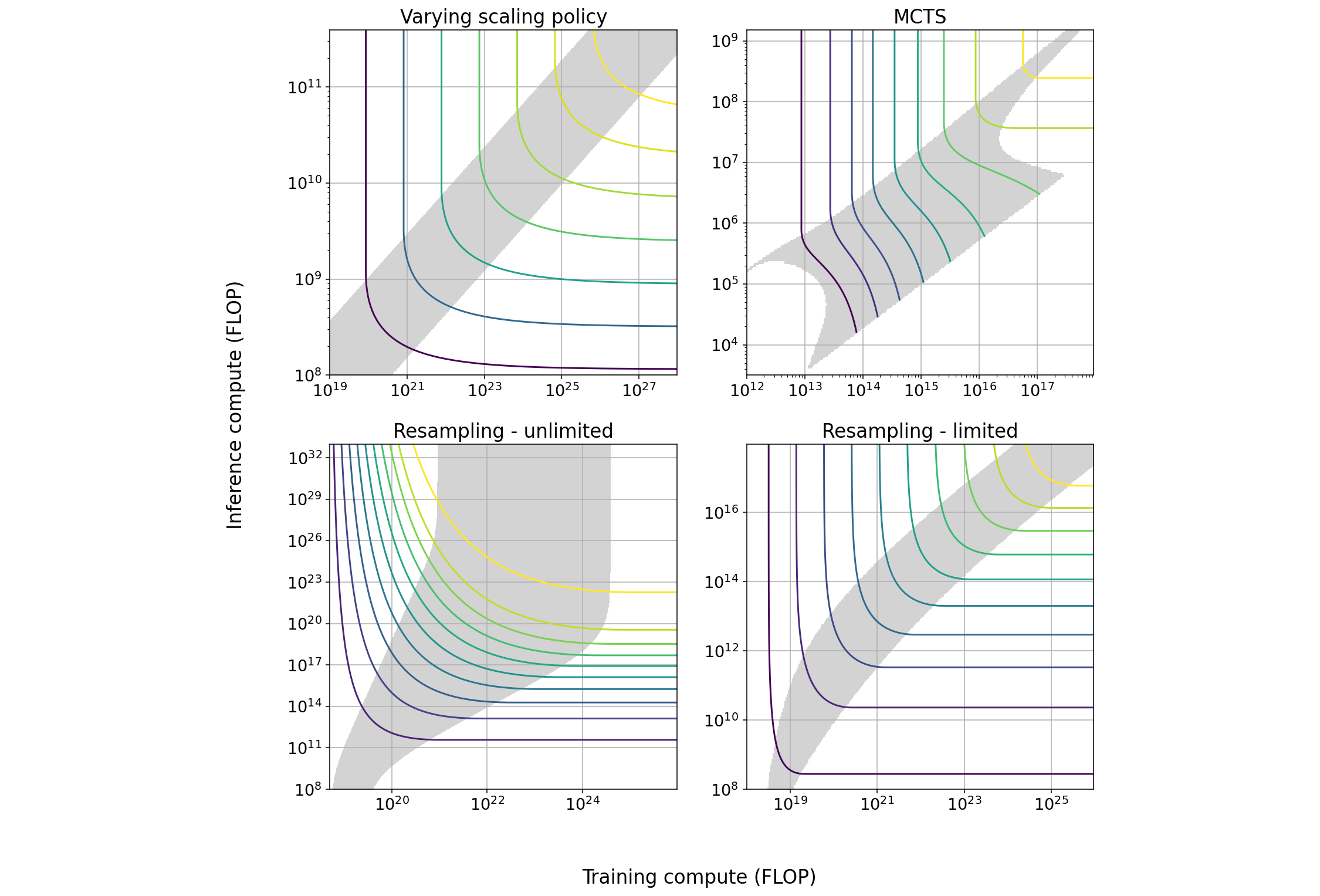
Figure 3: Possible ways of extending the regime of efficient (or linear) scaling and overcoming the latency wall. The blue line corresponds to multiplying all bandwidths (both memory and network) and dividing all latencies by a factor of 10.
Despite the modeling in the previous section seeming to set a hard upper bound on the scale of training runs, there are some foreseeable ways to potentially overcome these limits. One straightforward way is to simply reduce latency through hardware improvements, but as we’ve discussed previously, trends in latency improvement in past GPU generations have been disappointing.
The alternative is to keep the hardware the same, but change how we do training. Let’s recall the upper bound on the number of parameters coming from the latency wall:
\[N \leq \frac{t_{\text{train}} \cdot B}{80 \cdot n_{\text{layer}} \cdot t_{\text{latency}}}\]Because we derived this bound by assuming Chinchilla scaling, one immediate solution for getting past the latency wall is to undertrain models: in other words, train a model with \(N\) parameters on fewer than \(20 \cdot N\) tokens. This would work, as it would mean fewer forward and backward passes need to be performed in the fixed time window devoted to training, alleviating both bandwidth and latency constraints. However, the Chinchilla scaling law implies that such a policy would result in a worse conversion rate of training compute to model capabilities. As a result, we do not consider this a plausible scenario for overcoming the latency wall.
If we wish to increase this upper bound without compromising the logical integrity of the training process, and we’re not willing to undertrain our models, we can either increase the variables in the numerator or reduce the variables in the denominator. Because \(t_{\text{latency}}\) is fixed by hardware and \(t_{\text{train}}\) is assumed to be constant, the only two levers available to us are increasing the batch size and reducing model depth:
Increasing the batch size
If we can find a way to aggressively scale batch sizes together with model sizes, we can push out the latency wall. This also gives us greater opportunities to do data and pipeline parallelism, thereby also pushing out the point at which memory or network bandwidth issues would become a serious constraint. The problem with this approach is that in practice, scaling batch sizes beyond some point called the critical batch size hits diminishing returns.
McCandlish et al. (2018) note that the critical batch size increases with model performance, and since bigger models perform better later in training this suggests bigger language models should be able to accommodate larger batch sizes. This seems promising, and according to their model, the critical batch size should scale with the reciprocal of the reducible loss of the model. Based on this, and drawing on the scaling law from Hoffmann et al. (2022), our mainline results in the model already allow for a scaling of \(B \sim N^{\frac{1}{3}}\). Pushing out the latency wall beyond \(\sim 7e31 \text{ FLOP}\) requires even more aggressive scaling than this.
A recent paper which was published only a few days before the publication of our own work, Zhang et al. (2024), finds a scaling of \(B = 17.75 \cdot D^{0.47}\) (in units of tokens). If we rigorously take this more aggressive scaling into account in our model, the fall in utilization is pushed out by two orders of magnitude; starting around \(3e30 \text{ FLOP}\) instead of \(2e28 \text{ FLOP}\). Of course, even more aggressive scaling might be possible with methods that Zhang et al. (2024) do not explore, such as using alternative optimizers.
Overall, if the latency wall is overcome by algorithmic innovations, we think the most plausible candidate that could be responsible is some way to scale training batch sizes more aggressively than we have assumed.
Reducing the model depth
The alternative to scaling the batch size more aggressively is to scale model depth less aggressively. The literature on scaling laws separately taking model depth and width into account is surprisingly thin, and so the best we can do to infer current best practices in the field is to consult papers which train a lot of models at different scales, such as Hoffmann et al. (2022).
A scaling law estimated on the models trained in Hoffmann et al. (2022) gives that \(n_{\text{layer}} \sim N^{0.27}\) or so, which is close to the \(N^{\frac{1}{3}}\) scaling we assume for the critical batch size in our model, and so the two effects roughly cancel each other out. However, Hoffmann et al. (2022) do not perform any tests to see if this scaling policy is optimal, and they have no scaling law which can be used to quantify the cost of deviating from any optimal policy. As a result, this can at best be considered weak evidence for how we can expect model depth to be scaled in the future.
If it’s feasible to keep model depth roughly the same while continuing to scale batch sizes at the expected rate, the latency wall can be pushed out by many orders of magnitude of training compute. We consider this a less plausible scenario than simply scaling batch sizes more aggressively.
Conclusion
Our model suggests that the the linear scaling regime of increasing model scales and cluster sizes without substantial declines in utilization will come to an end at a scale of around \(2e28 \text{ FLOP}\) in a business-as-usual scenario. With the largest known model so far being estimated to have used around \(5e25 \text{ FLOP}\), and with the historical rates of compute scaling of around 4-5x per year, we’ll hit the \(2e28 \text{ FLOP}\) threshold in around 3 years.
Pushing this threshold out by hardware improvements seems challenging, even by just one order of magnitude. This is because we need substantial and concurrent improvements in memory bandwidth4, network bandwidth, and network latency. In contrast, the more promising way to overcome this threshold appears to be more aggressive scaling of batch sizes during training. The extent to which this is possible is limited by the critical batch size, whose dependence on model size for large language models is currently unknown to us, though we suspect leading labs already have unpublished critical batch size scaling laws.
Critical batch size scaling laws, model depth & aspect ratio scaling laws, and sparsity factor scaling laws (e.g. for MoE models) are all important for understanding the future of distributed training, and there is little solid published research on any of them. Our understanding of the future of distributed training would be greatly improved if we had more reliable research on these questions.
You can learn more about data movement bottlenecks and our work in our paper.
-
While there are engineering issues that must be overcome, e.g. because many GPUs in a cluster will fail throughout the course of a longer training run, these pose no fundamental limits to scaling. As long as a model and its optimizer states can fit inside the memory of our GPUs, there’s no barrier to just training bigger models for longer. ↩
-
For example, when multiplying two \(d \times d\) square matrices, we need to do \(\sim 2d^3\) FLOP but \(\sim 3d^2\) memory reads & writes. As \(d\) is scaled down, the former decreases more rapidly than the latter. ↩
-
In practice, things might be worse than this. For instance, NCCL’s tree-based all-reduce protocol across nodes does not have constant latency, but latency that scales with the logarithm of the number of nodes participating in the all-reduce. However, in principle this logarithmic scaling can be eliminated by using e.g. a mesh topology. ↩
-
Assuming model weights are not stored in SRAM. While it might seem implausible that this would ever be viable, we think cluster sizes growing more quickly than model sizes makes SRAM a viable option in the future if the parallelism scheme used for training is appropriately chosen. ↩