Predicting GPU Performance
We develop a simple model that predicts progress in the performance of field-effect transistor-based GPUs under the assumption that transistors can no longer miniaturize after scaling down to roughly the size of a single silicon atom. Our model forecasts that the current paradigm of field-effect transistor-based GPUs will plateau sometime between 2027 and 2035, offering a performance of between 1e14 and 1e15 FLOP/s in FP32.
Published
Resources
Executive summary
We develop a simple model that predicts progress in the performance of field-effect transistor-based GPUs under the assumption that transistors can no longer miniaturize after scaling down to roughly the size of a single silicon atom. We construct a composite model from a performance model (a model of how GPU performance relates to the features of that GPU), and a feature model (a model of how GPU features change over time given the constraints imposed by the physical limits of miniaturization), each of which are fit on a dataset of 1948 GPUs released between 2006 and 2021. We find that almost all progress can be explained by two variables: transistor size and the number of cores. Using estimates of the physical limits informed by the relevant literature, our model predicts that GPU progress will stop roughly between 2027 and 2035, due to decreases in transistor size. In the limit, we can expect that current field-effect transistor-based GPUs, without any paradigm-altering technological advances, will be able to achieve a peak theoretical performance of 1e14 and 1e15 FLOP/s in single-precision performance.
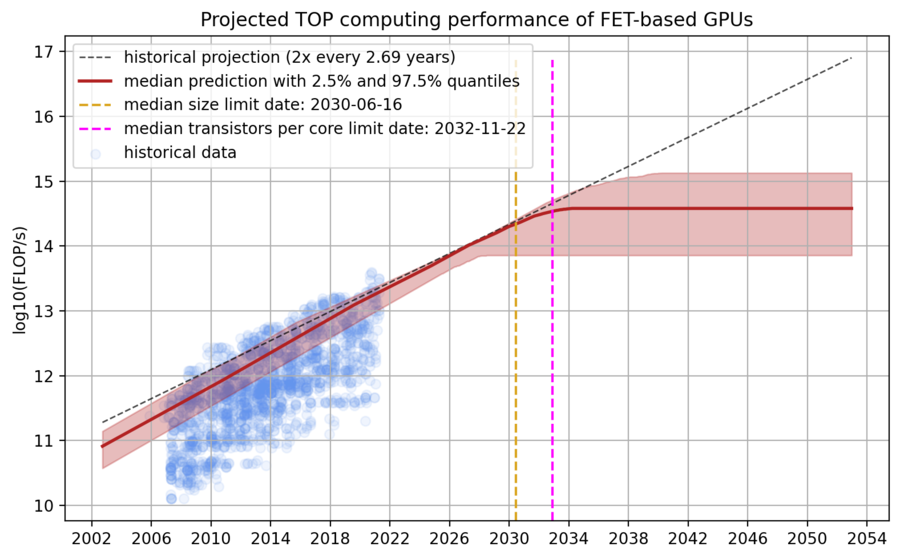
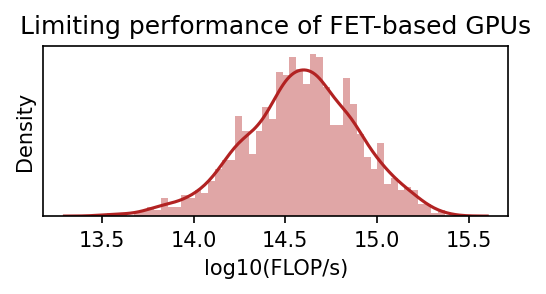
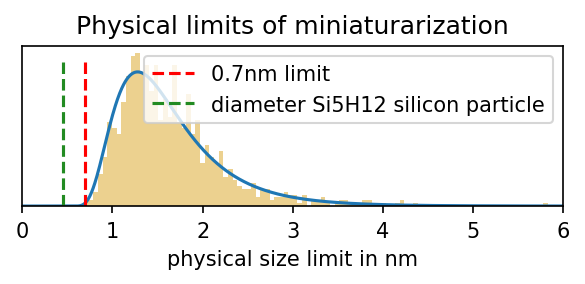
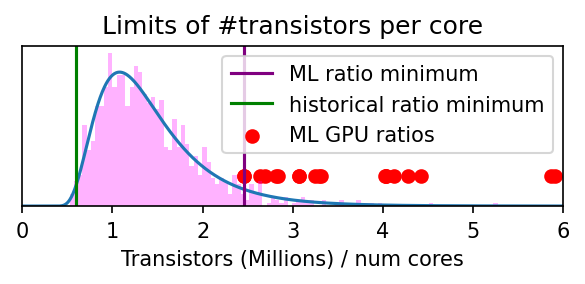
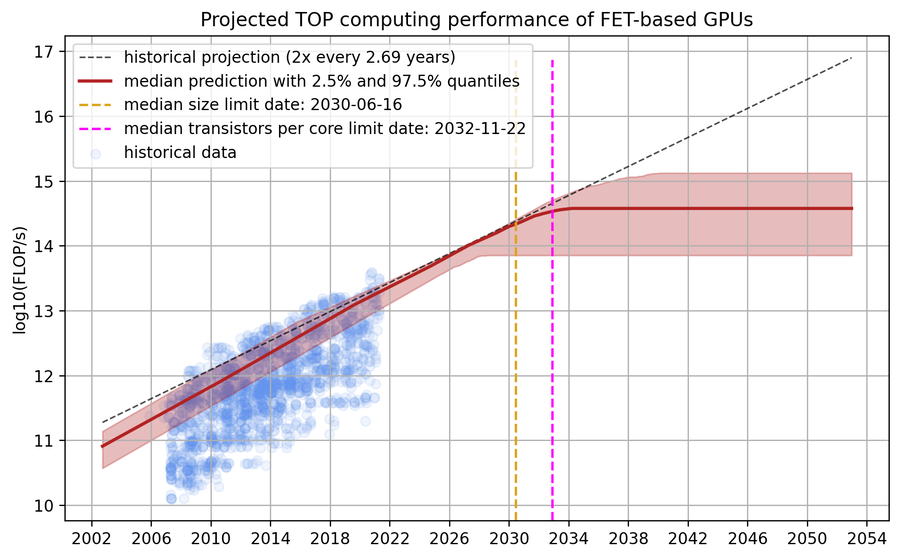
Figure 1. Model predictions of peak theoretical performance of top GPUs, assuming that transistors can no longer miniaturize after scaling down transistors to around 0.7nm. Left: GPU performance projections; Top right: GPU performance when the limit is hit; Middle right: Our distribution over the physical limits of transistor miniaturization; Bottom right: Our distribution over the transistors per core ratio with relevant historical comparisons.
While there are many other drivers of GPU performance and efficiency improvements (such as memory optimization, improved utilization, and so on), decreasing the size of transistors has historically been a great, and arguably the dominant, driver of GPU performance improvements. Our work therefore strongly suggests that it will become significantly harder to achieve GPU performance improvements around the mid-2030s within the longstanding field-effect transistor-based paradigm.
Introduction
As field-effect transistors (FETs) approach the single-digit-nanometer scale, it is almost certain that transistors will run into physical limits that prohibit further miniaturization. Many constraints on further miniaturization have been discussed in the literature, such as thermal noise voltage (Kish, 2001), reliability constraints stemming from imperfections in photoresist processes and random variations in photons (Neisser, 2021), and quantum tunneling (Markov et al., 2019; Frank et al., 2001), among others. These constraints have informed the timelines for the ending of sustained performance improvements driven by miniaturization. For example, the 2022 IRDS roadmap suggests that “ground rule scaling is expected to slow down and saturate around 2028”; similar predictions are offered elsewhere (e.g., Dammel, 2021 and Burg, 2021).
It is less clear how powerful hardware might be in the limit of what is permitted by physical constraints on transistors. Intel, based on internal analysis, projects that chips will be able to perform 1e15 FLOP/s around the year 2030 (Kelleher, 2022). By considering a variety of physical and manufacturing constraints, Veedrac, 2021 argues that improvements in transistor density of 20- to 100-fold are likely achievable, depending on whether or not 3D integration could succeed in producing die stacks with some minimal overheads for wiring and power. Cotra (2020), by considering multiple sources of improved hardware price-performance including transistor scaling, hardware specialization, and additional economic efficiency improvements, argues that improvements in the price of compute—specifically, the amortized costs of computation—will level off after around six orders of magnitude relative to 2020.
We provide a formal model of hardware performance that incorporates physical constraints on transistor scaling. Our work is organized as follows. First, we present a simple model of GPU performance, which consists of a performance model (a model of how GPU performance relates to the features of that GPU) and a feature model (a model of how GPU features change over time given the constraints imposed by the physical limits of miniaturization). We discuss the physical limits of transistor miniaturization and argue that transistor miniaturization will likely halt at or before the point when key dimensions of transistors shrink down to 0.7nm. We describe our estimates and present the GPU performance in FLOP/s predicted by our model over the next three decades. We conclude with a discussion of the limitations of our work.
A simple model of GPU performance
We use a composite of two simple models to generate predictions of GPU performance. The first relates the performance of GPUs to their features (such as the size of transistors, number of cores, etc.). The second is a model that projects historical trends in these features and takes physical limits on transistor scaling into account.
Let
where
where
In doing so, we have constructed a simple model of the evolution of hardware performance that accounts for how chip features relate to hardware performance while incorporating information about the limits on these chip features that are implied by physical limits. The following sections describe the setup of the model and the appendices provide more details.
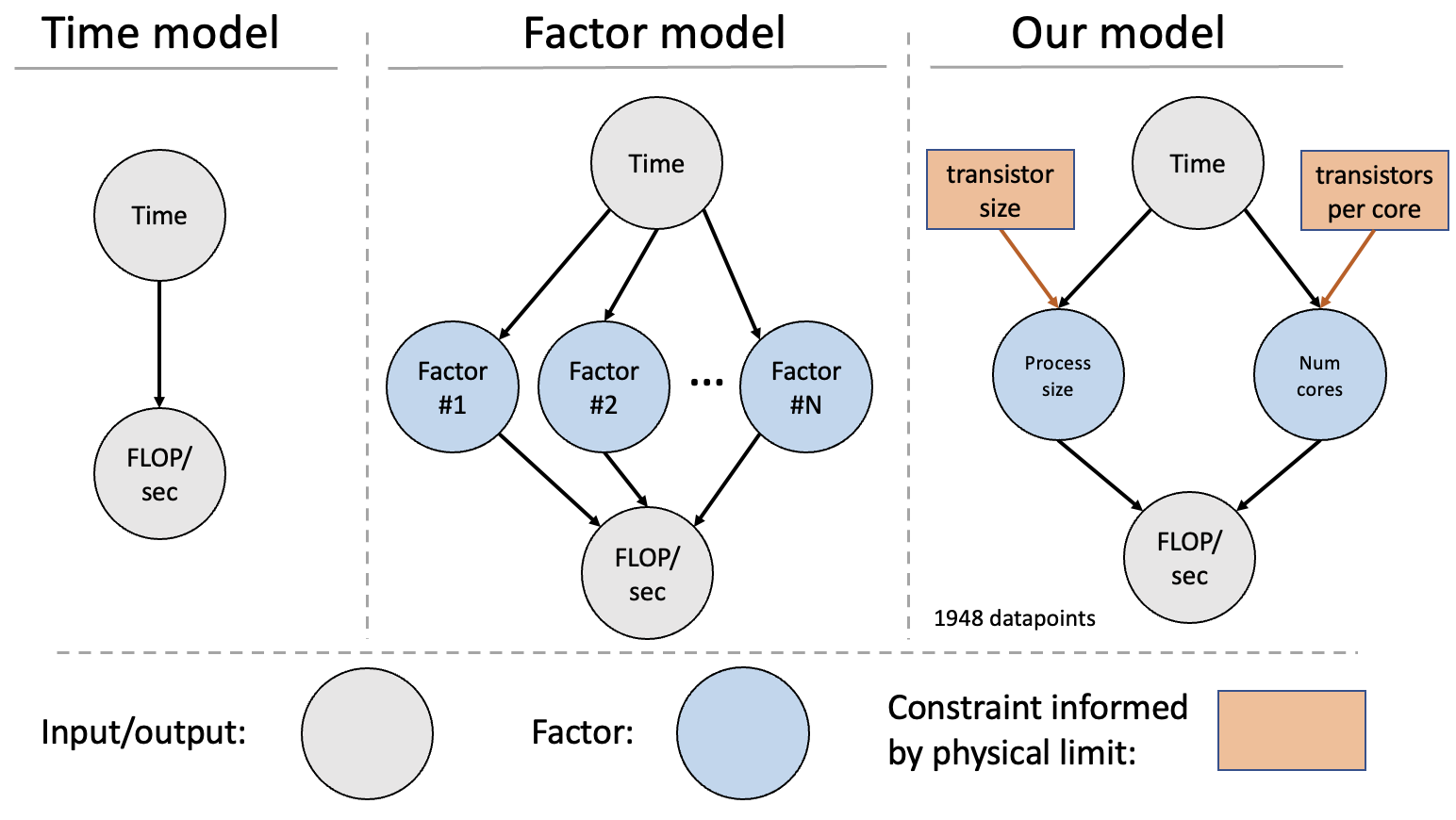
Figure 2: Overview of different approaches to modeling GPU performance. In this piece, we choose a factor model with two variables (process size and number of cores) and include the limits of miniaturization.
Feature and model selection
We want to select features that have a causal effect on FLOP/s such that changes in the factors actually translate into changes in FLOP/s. We, therefore, start with a pool of 21 criteria and narrow them down by using the following desiderata:
- The feature is predictive of GPU performance and there should be a causal relation between this feature and FLOP/s. There should be a well-understood causal relationship that explains why an increase in the values of the feature leads to an increase in FLOP/s (rather than being an effect of, or having a common cause with, FLOP/s).
- The features themselves should be relatively predictable. Specifically, we have a preference for features that improve predictably and regularly over time, and whose variance is small at any point in time (so that each contemporary GPU is relatively similar on that dimension), enabling us to more confidently predict the characteristics of future GPUs.
- The burden is on inclusion, not exclusion. We have a preference for simpler models, given overfitting could severely harm out-of-distribution performance. As a result, we rely on the Bayesian Information Criterion (which strongly punishes model complexity) for model selection.
For more details, see Appendix A - feature selection. We find that six features satisfy these desiderata: number of cores, process size (in nm), GPU clock (in MHz), bandwidth (in GB), memory clock (in MHz) and memory size (in MB). For many years now, the clock speed of CPUs and GPUs has only marginally increased or plateaued. Therefore, we think that transistor size and the number of cores are the two key drivers of progress, and clock speed is less important. We think of the first three features as primary variables, (i.e., an increase in the feature directly improves performance), and of the last three features as secondary variables, (i.e., an increase in the feature doesn’t always improve performance but it supports the scaling of a primary variable).
We prefer simpler models for improved interpretability and their reduced likelihood of overfitting the data and thereby producing worse predictions. We select which features to include based on the Bayesian Information Criterion (BIC). We find that our performance model fits the data the best with two features: transistor size1 and number of cores. Moreover, since many factors are strongly correlated with one another, the inclusion of additional features also increased the error bars on the estimates of the relevant coefficients. Therefore, we refrain from adding more than two components.
For all components, we use a log-linear fit, e.g., log(feature) ~ time, as a baseline and compare it with different polynomial and sublinear fits of the data. We find that, in all cases, none of the more complex models has a tangible increase (measured as a 0.01 increase in r-squared) over the basic log-linear model. Therefore, we chose to stick with the most obvious log-linear model for all components. See Appendix B for more details.
One could argue that GPU size, and especially die size, increase over time, and our model does not explicitly account for that. However, we think that a) die size is already implicitly accounted for in the number of cores since the number of cores grows faster than the transistor size decreases, b) even if they were unaccounted for, increasing die size would not increase predicted limiting performance substantially and c) larger GPUs might improve performance but not price-performance which is, in some sense, ultimately what matters for compute progress. We provide a detailed analysis of these arguments in Appendix E.
Physical limits of transistor miniaturization
There have been multiple estimates of physical size limits of field-effect transistors (see table in Appendix C). In our projections, we enforce a prior over the miniaturization limits of FET-transistors (See Figure 3). This range coincides with the range—roughly between 0.7nm and 3nm—that was constructed by surveying existing research on the physical limits of transistors, with the exception that we did not assign much weight to purely proof-of-concept results (such as, for example, single-atomic-layer FinFETs), where we expect reliability and performance issues to be major obstacles to mass-production.

Figure 3: Distribution over the limits of miniaturization we use in our model. The parameters of the distribution are chosen to reflect what we think of as a hard boundary at 0.7nm and such that most probability mass is smaller than 3nm. We use a log-normal distribution with mu=0, sigma=0.5 and shift it by 0.5 to the right.
We found that, historically, process size and the minimum dimension of the transistor very strongly correlate and, therefore, extrapolating either produces very similar predictions (see Figure 4 and Appendix D). We chose to keep process size as the predictive factor for two reasons. First, we think it’s not clear that the minimal dimension of a transistor is a better measurement than process size. Just because the smaller dimension has hit its limit does not mean the larger dimension has. Second, we have very few data points for FinFET-based GPUs. Thus, predictions based on them might be misleading or inaccurate. For the rest of the report, you can thus think of “process size” as an approximation to transistor size.
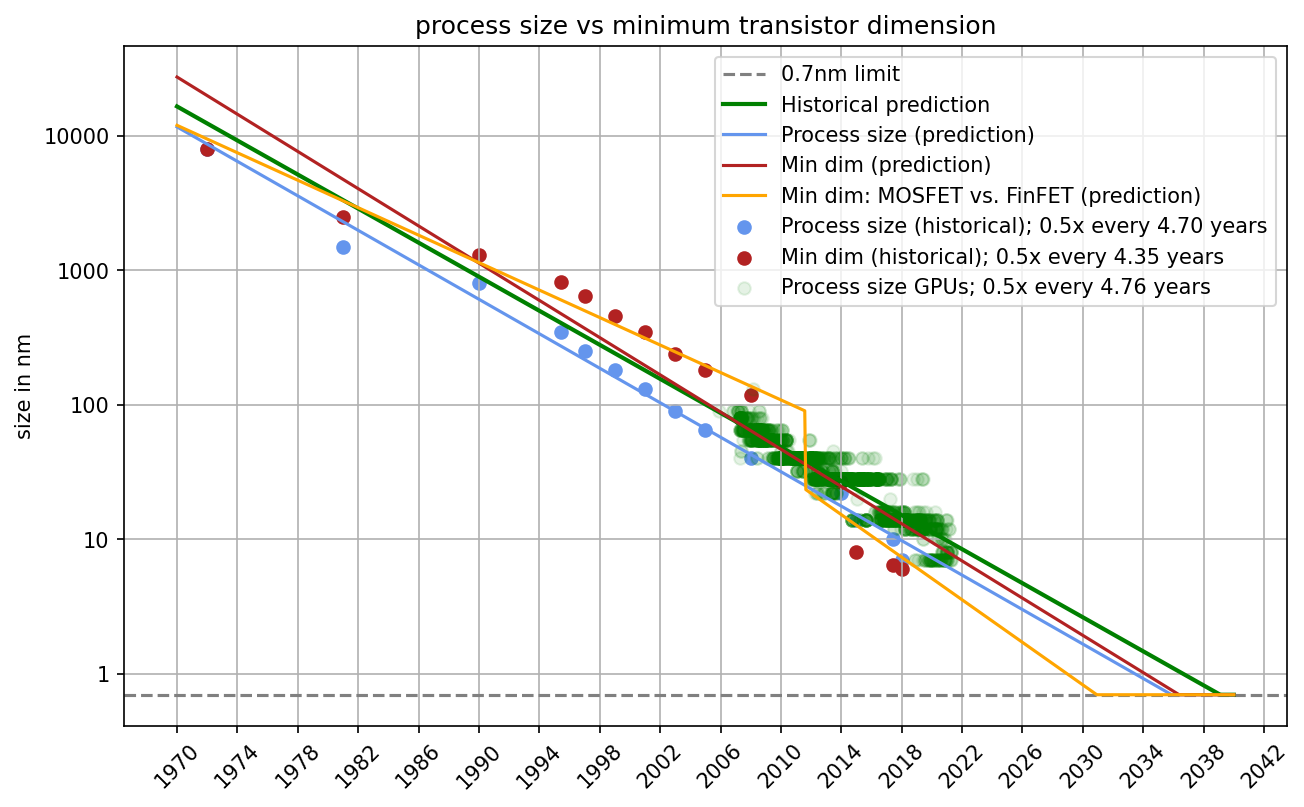
Figure 4: Comparison of process size and minimum transistor dimension. We find that both scale very similarly even when we account for a MOSFET vs FinFET distinction. Therefore, we conclude that we can use process size as a decent approximation for transistor size in the rest of this piece.
Limits on the number of cores
Once the physical limit of transistor size is hit, transistor miniaturization ceases to be feasible. However, increasing the number of cores on the chip is still possible, which improves performance by enabling more effective parallel computation. When the number of transistors ceases to increase, we expect that the number of cores will continue growing until it hits the limit of the number of transistors required to produce high-performing cores.
We enforce a prior over the number of transistors per core that is informed by our dataset (see Figure 5). Specifically, we find that the minimum number of transistors per core has been 600k, while this minimum ratio of GPUs used in ML (where workloads are generally highly parallel) is on the order of 2.4M.2

Figure 5: With the information from the previous figure, we construct a distribution that reflects our best guess of what the limit of the number of transistors per core is. We think it is likely lower than what current state-of-the-art ML GPUs can achieve (since they are likely not optimized for that ratio) but a bit higher than the historical minimum. We use a log-normal distribution with parameters mu=0.3 and sigma=0.5
Predictions
We predict the performance of TOP GPUs from quantile regressions of the historical data that take the two limits into account, i.e., the physical size limit of transistors and the number of transistors per core. Concretely, we fitted a 5th percentile quantile regression for the log10(process size) ~ time model (because smaller transistors imply higher performance) and a 95th, 90th, 85th and 80th percentile quantile regression for the log10(number of cores) ~ time model. We then draw uniformly from these four regressions. The reason we fitted multiple quantile regressions for the cores model is that they yield different slopes (rather than just different intercepts), and we have no strong reason to prefer one slope over the other. The predictions that result from these two regressions are then fed into the performance model. Additionally, we draw samples from the distributions over the transistor miniaturization limit and the transistors per core limit and adapt the projections accordingly. This process is repeated 1000x times and yields the distribution over projections that can be seen in the next figure. More details can be found in Appendix B.
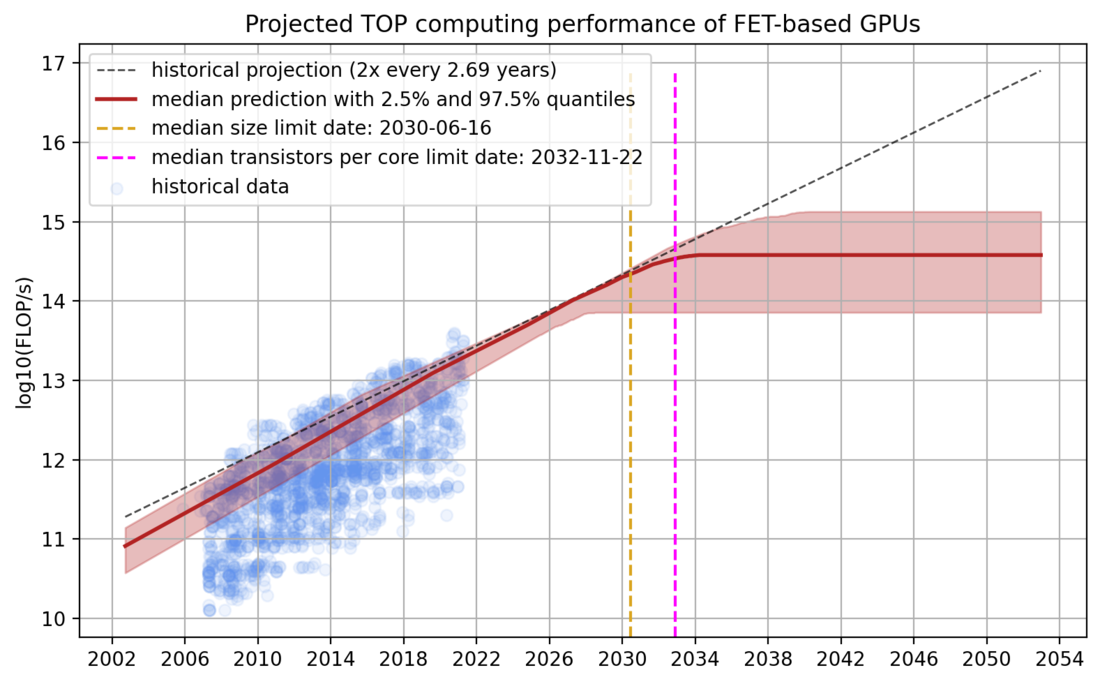
Figure 6: A distribution over projections of TOP GPU performance. The historical projection comes from a 90th-percentile regression of the dataset. The model predicts that the median dates for the two limits are ~2030 and ~2033 and that the limiting performance is between 1e14 and 1e15 FLOP/s.
Every predicted trajectory has two kinks: the first corresponding to when the physical limit of transistor size is hit, and the second when the number of transistors per core can no longer be decreased without losses in performance. After the second limit is hit, our predicted trajectory is flat because there are no further avenues of progress from the two factors our model considers.
Our model predicts that the median dates for the two limits are 2030 and 2033. Furthermore, the model predicts that the performance limit is hit between 2027 and 2035 with a maximum performance of 1e14 and 1e15 FLOP/s. If we assume constant prices and an amortization period of three years, this would mean that the price per FLOP for the limiting GPUs based on field-effect transistors is between 1e22 FLOP/$ and 1e23 FLOP/$.3
Limitations
In this work, we make a lot of assumptions that lead to limitations:
- We assume the developments in transistor size continue as they did in the last 15 years. However, there might be reasons to assume that this speed will decelerate, e.g., R&D spending can’t continue exponentially, ideas are getting harder to find, etc.
- We don’t make any claims about limits other than size. In particular, we have not explicitly factored in heat dissipation, but some of the estimates we base our distribution over limits on implicitly include limits from heat dissipation.
- This prediction is only applicable to the current paradigm of GPUs. Our predictions don’t make claims about other paradigms such as quantum computing or neuromorphic computing.
- We do not account for the possibility of 3D chip designs improving GPU performance
- We assume the number of transistors per core is lower-bounded by roughly the minimum transistors per core that we have historically seen. However, computer architects might focus on reducing the number of transistors per core beyond its historical limit once miniaturization is no longer feasible.
- We assume that you can scale the number of cores by at least a few orders of magnitude without drops in performance. This assumes that ML algorithms can be parallelized to a massive extent. We are not sure this is true, even though most current ML progress is based on parallelization.
Appendix A - Feature selection (details)
Our dataset includes ~150 features for GPU and CPU progress. Of these, we choose the 21 features that have a plausible chance (as judged by us) of being relevant to predict GPU progress. We then reduce these features to the most important ones with the following strategies.
Correlation with FLOP/s
As a first selection criterion, we measure the correlation between the feature and FLOP/s. We remove all features from the pool that have a correlation coefficient between -0.5 and 0.5. Our reasoning is that a strong predictor should be decently correlated with the variable it predicts, but this specific threshold is ultimately arbitrary.
We compute this correlation for different transformations of the data, i.e., all combinations of linear and log10 as shown for the example of num_shading_units in the following figure.
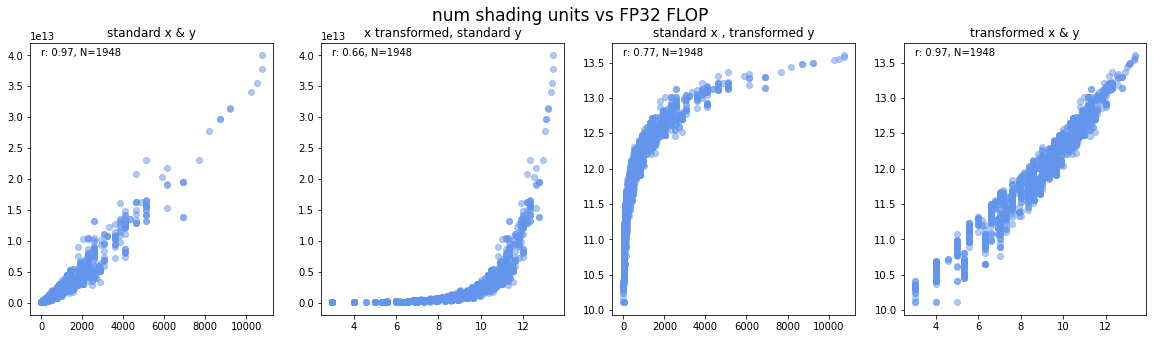
Figure 7: Correlations of features with performance (in FLOP/s) for different transformations of the data. In the example of the number of shading units, log transformations of both variables seem to give the best fit.
After this process, we have 16 variables left. In all excluded cases, we also manually looked at the data to see if we were missing obvious transformations that would lead to inclusion.
Consistent correlation with time
Since we ultimately want to make predictions far into the future, every variable has to correlate with time consistently, e.g., later dates consistently imply an increase in log10(num_cores). We operationalize this by building a linear model log(feature) ~ time and excluding every variable with an r-squared value of less than 0.3. Using a log-linear model also ensures that the variation of the feature is over time and not over the feature. In the following figure, you can see an example of how the number of shading units changes over time.
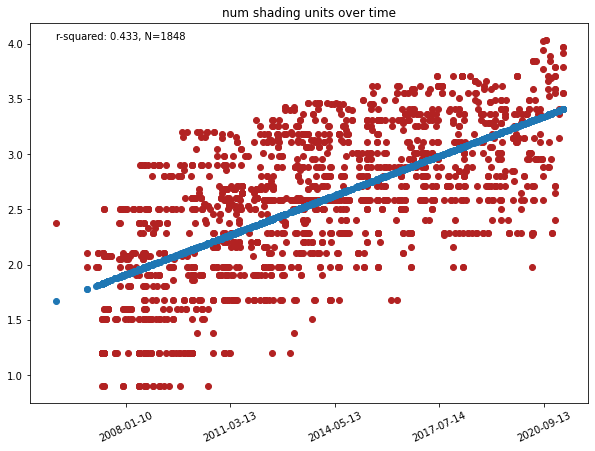
Figure 8: The number of shading units over time. We find that it consistently increases with time which means it fulfills one of our desired criteria.
After this process, we are left with nine variables. In all excluded cases, we also manually looked at the data to see if we were missing obvious transformations that would lead to inclusion.
Identifying causal relationships
We want to build a predictive model for future progress in GPU. Therefore, we have to ensure that every feature we selected has a plausible causal story for increasing FLOP/s. Concretely, for the nine remaining variables, this means:
- Num_cores: More cores means more parallelization means more FLOP/s
- GPU_clock_in_MHz: Higher frequencies directly imply more FLOP/s
- process_size_in_nm : Smaller transistors imply more transistors per GPU imply more FLOP/s
- bandwidth_in_GBs: a bottleneck in bandwidth can translate into a bottleneck in FLOP/s
- memory_clock_in_MHz: a bottleneck in memory clock can translate into a bottleneck in FLOP/s
- memory_size_in_MB: a bottleneck in memory size can translate into a bottleneck in FLOP/s
- Transistors_in_millions (remove): While more transistors imply more FLOP/s, they are a downstream effect of smaller transistors. Since it is therefore strongly correlated with process_size, we remove this variable.
- Num_shading_units (remove): Shading units are specialized units for improved shading properties, e.g., in video games. There is no causal story from num_shading_units -> FLOP/s and we, therefore, remove it.
- Num_compute_units (remove): While more compute units likely imply more FLOP/s, they are effectively a superclass of num_cores. We think num_cores is the more relevant variable and thus remove num_compute_units.
Remaining variables
There are six remaining candidate variables that passed all of the previous exclusion criteria. We think they can be grouped into two different classes.
Primary variables: these are variables where an increase in the variable directly translates into more FLOP/s. Concretely, these are num_cores, process_size_in_nm and GPU_clock_in_MHz.
Secondary variables: these are variables that can limit FLOP/s if they are too low, but an increase in the variable doesn’t directly translate to more FLOP/s. For example, low bandwidth reduces effective FLOP/s but increasing bandwidth doesn’t increase effective FLOP/s after a threshold is passed. Concretely, these variables are bandwidth_in_GBs, memory_clock_in_MHz and memory_size_in_MB.
Our variables correlate strongly with each other. This has implications for building our final model.
| GPU |
num |
process |
memory |
memory |
bandwidth |
|
| GPU |
1.00 | 0.58 | -0.60 | 0.52 | 0.61 | 0.46 |
| num |
0.58 | 1.00 | -0.64 | 0.82 | 0.69 | 0.85 |
| process |
-0.60 | -0.64 | 1.00 | -0.76 | -0.70 | -0.64 |
| memory |
0.52 | 0.82 | -0.76 | 1.00 | 0.64 | 0.80 |
| memory |
0.61 | 0.69 | -0.70 | 0.64 | 1.00 | 0.69 |
| bandwidth |
0.46 | 0.85 | -0.64 | 0.80 | 0.69 | 1.00 |
Appendix B - model selection
This section describes the model building in more detail.
Testing non-linear fits
For the six remaining variables, we wanted to make sure that the linear fit on log data actually captures all relevant trends. Therefore, we compared the respective model fit with a linear+square fit, a linear+log fit and a linear+square root fit. In all cases, we could not see any significant improvements compared to the linear baseline.
Furthermore, adding a second term into the prediction model usually led to implausible future predictions, e.g., adding a logarithmic term implies that the trajectory is decreasing below current performance levels in the future. Since this is clearly implausible, we decided to use the linear fit on log data in all cases.
Our model
From the remaining six variables, we built multiple models by combining different variables. In each case, we predict FLOP from the combination of variables and compare fit using r-squared values. We first chose each variable on its own and then looked at combinations of primary variables and all variables.
Model:
| Dependent variables (X) | r-squared | BIC |
|---|---|---|
| GPU_clock | 0.475 | 1343 |
| num_cores | 0.936 | -1281 |
| process_size | 0.508 | 2708 |
| memory_size | 0.729 | 1271 |
| memory_clock | 0.565 | 2051 |
| bandwidth | 0.802 | 755.2 |
| GPU_clock, num_cores, process_size | 0.947 | -1211 |
| GPU_clock, num_cores | 0.947 | -1218 |
| num_cores, process_size | 0.950 | -1753 |
| GPU_clock, process_size | 0.531 | 1224 |
| GPU_clock, num_cores, process_size, memory_size, memory_clock, bandwidth | 0.968 | -1665 |
While taking all variables produces the best overall fit (measured by r-squared), we decide to use num_cores+process_size as our model for the rest of the post. There are several reasons for this choice:
- Num_cores+process_size is only marginally worse than all variables combined, and it has a better BIC.
- There is a very high correlation between all predictive variables (see previous section). Thus, combining more variables increases the error of our prediction.
- Not all data points provide values for GPU_clock. Thus, the model that includes GPU_clock performs slightly worse than num_cores+process_size. This would be roughly half the datapoints we could use.
- We can tell a clear causal story for why num_cores and process_size are core drivers of GPU progress and will continue to be.
We want a model we can interpret and trust, and thus, settle on this choice. Our model, therefore, reflects the following combination of linear models:
- Factor models: log(num_cores) ~ time and log(process_size) ~ time
- Final model: log(FLOP) ~ log(num_cores) + log(process_size)
Modeling physical size limits of transistors
We think that the size of transistors will hit a physical limit at some point. In our estimation (see next section), we argue that this limit is roughly at 0.7nm, which is very close to the size of a silicon atom. We think it is possible that the limit will be hit earlier, e.g., due to heat or quantum tunneling, but we want to model a hard boundary in this piece. To visualize different examples of limits, consider the following figure.
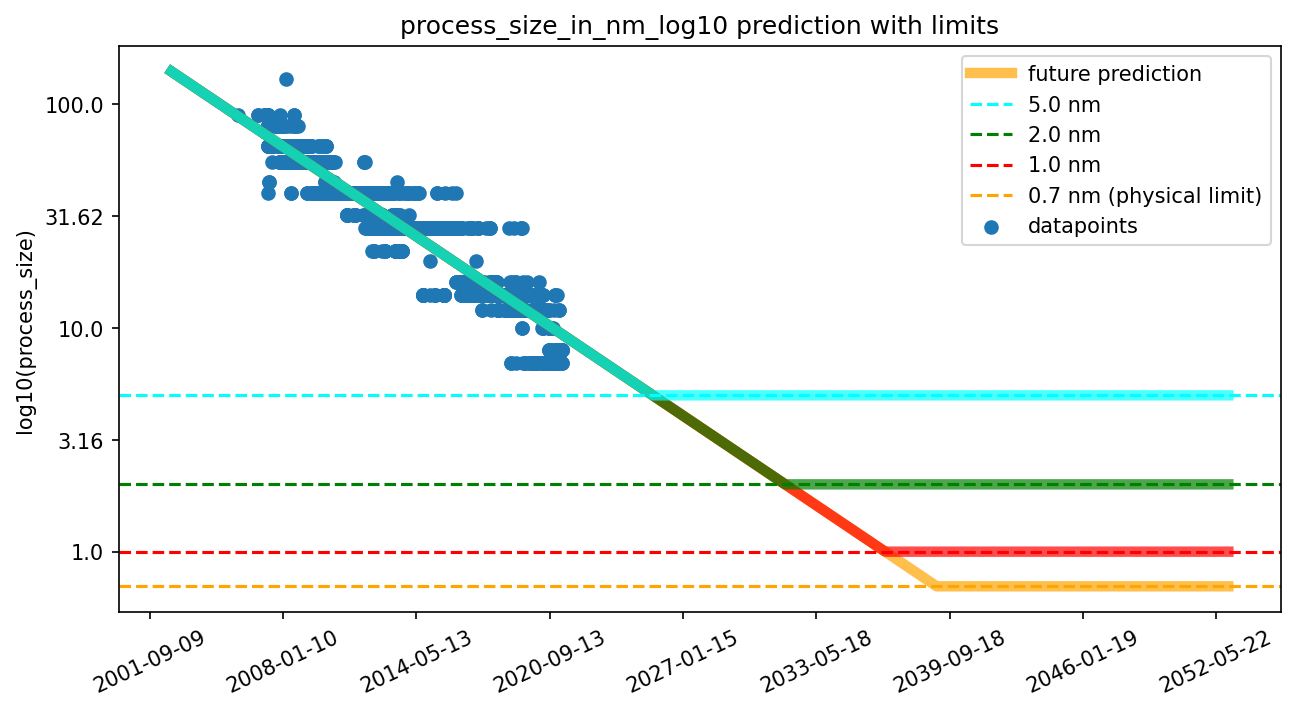
Figure 9: Projections from historical process size (as a proxy for transistor size) with different physical size limits.
To include our uncertainty about the boundary, we sample from a log-normal distribution over possible values of the limit as indicated in the following figure. We chose the parameters of the distribution such that the limit is below current capabilities but above the suggested physical limit. Interestingly, this distribution also aligns with the projected limit of quantum tunneling at 1-3nm.

Figure 10: The distribution over the physical size limits of miniaturization we use in our model. The distribution parameters are chosen to reflect what we think of as a hard boundary at 0.7nm and such that most probability mass is smaller than 3nm.
In practice, that means we project the future trajectory of process size from the historical trend and fix the date at which the limit is hit. All values after that date will be set to the limit, i.e., progress in transistor miniaturization is assumed to stop at that point.
Modeling limits of transistors per core
We think that after the miniaturization barrier is hit, some of the performance progress can be compensated by adding more cores. However, since progress in transistor size has stopped at this point, increasing the number of cores necessarily implies having fewer transistors per core. We think that this process will then hit another limit at which the number of transistors per core can’t be reduced anymore without a loss of performance.
Historically, this ratio has ranged from 600k transistors per core to 40M transistors per core. GPUs that have been used in state-of-the-art ML experiments have ranged from 2.6M to 12M transistors per core (see Figure below).
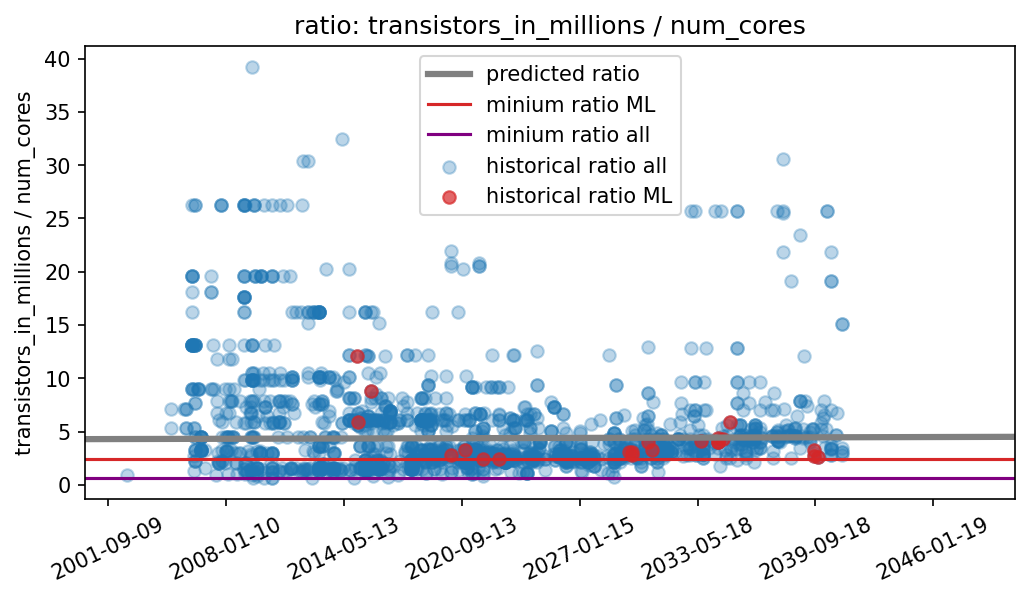
Figure 11: The ratio of transistors per core for all GPUs in our dataset. We highlighted GPUs that have been used for large ML experiments in the past to see if they are outliers in a specific way, but think they basically follow a similar trend as all other GPUs. Furthermore, we have added lines to indicate the minimum ratio for all GPUs, for ML GPUs and the predicted ratio from a linear model.
Therefore, we expect this limit to be somewhere between the historical limit and the limit for current ML GPUs. However, since we are unsure about the exact physical constraints, our model additionally contains values outside of the historical constraints (see next figure).

Figure 12: With the information from the previous figure, we construct a distribution that reflects our best guess of what the limit of the number of transistors per core is. We think it is likely lower than what current state-of-the-art ML GPUs can achieve (since they are likely not optimized for that ratio) but a bit higher than the historical minimum.
We include this constraint in our model by adding a second limit that lower-bounds the number of transistors per core.
Combining this into a model
In this piece, we want to primarily model the performance of TOP GPUs, i.e., those GPUs that set a new state-of-the-art for performance. Additionally, we add two analyses of other possible predictions, one for the median GPU and one for the median GPU when we model MOSFET and FinFET separately. We think these analyses are much less important but see them as an interesting robustness test.
In all cases, you can observe two kinks in the model. The first kink is when the prediction hits its respective physical size limit. After the first kink, all further progress is solely determined by adding more cores to the GPU. The second kink is hit when the limit of transistors per core is reached. After that, the trajectory is flat since both limits have been hit. The predicted trajectories in the following figures show examples of the two kinks.
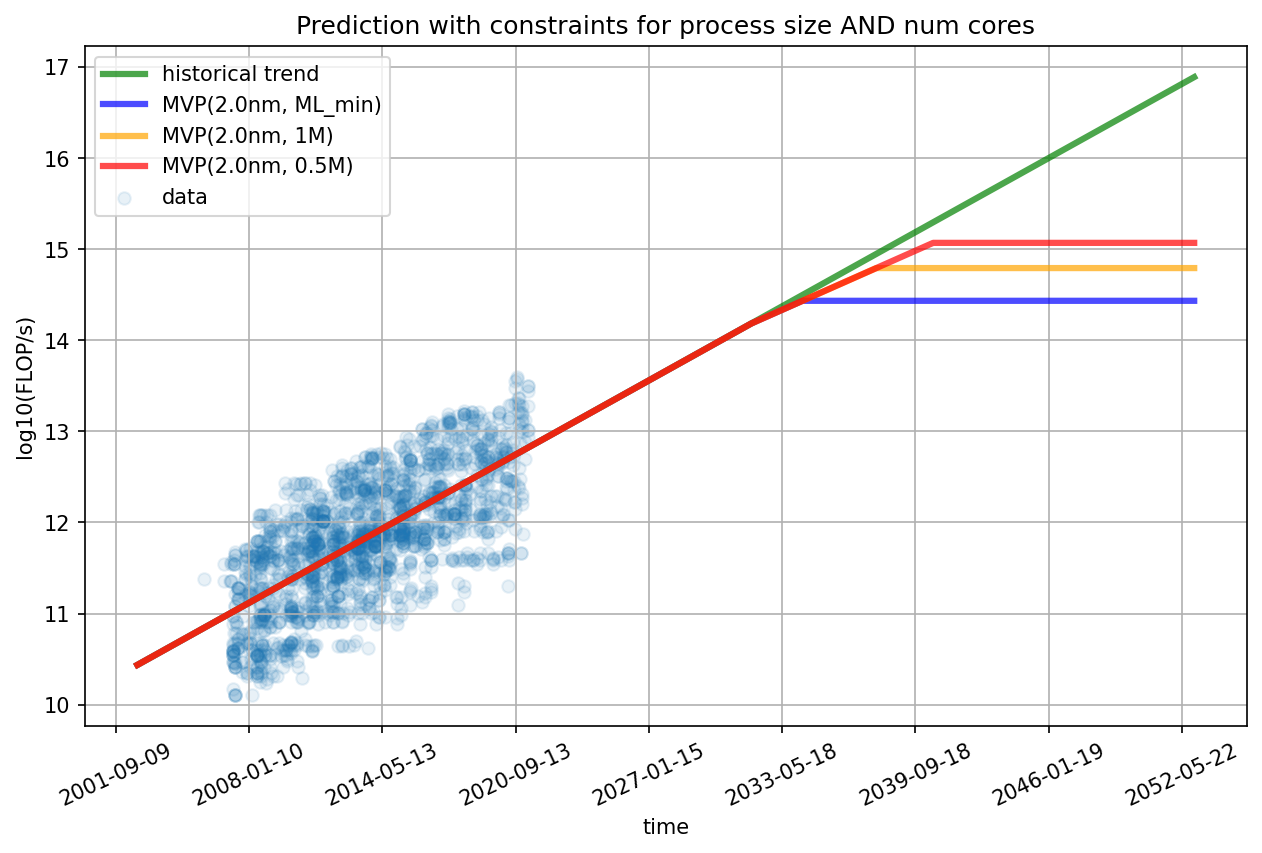
Figure 13: Examples of projections with different constraints. All trajectories assume a miniaturization limit of 2nm and a transistors-per-core limit of 2.6M (ML_min), 1M and 0.5M respectively. The main purpose of this figure is to show the two kinks that correspond to the two limits being hit.
To predict the TOP GPUs, we draw samples from the distributions over the transistor size limit and the transistors per core limit. Furthermore, we fit a 5th-percentile regression for transistor size (remember that smaller is faster) and do a 95th, 90th, 85th or 80th percentile regression for the number of cores. As you can see in the following figure, choosing different values for the quantile regression has a clear effect on the slope of the prediction, and thus, the projected date of the limit. We thus draw different samples because we have uncertainty about which of them models the TOP performance most accurately.
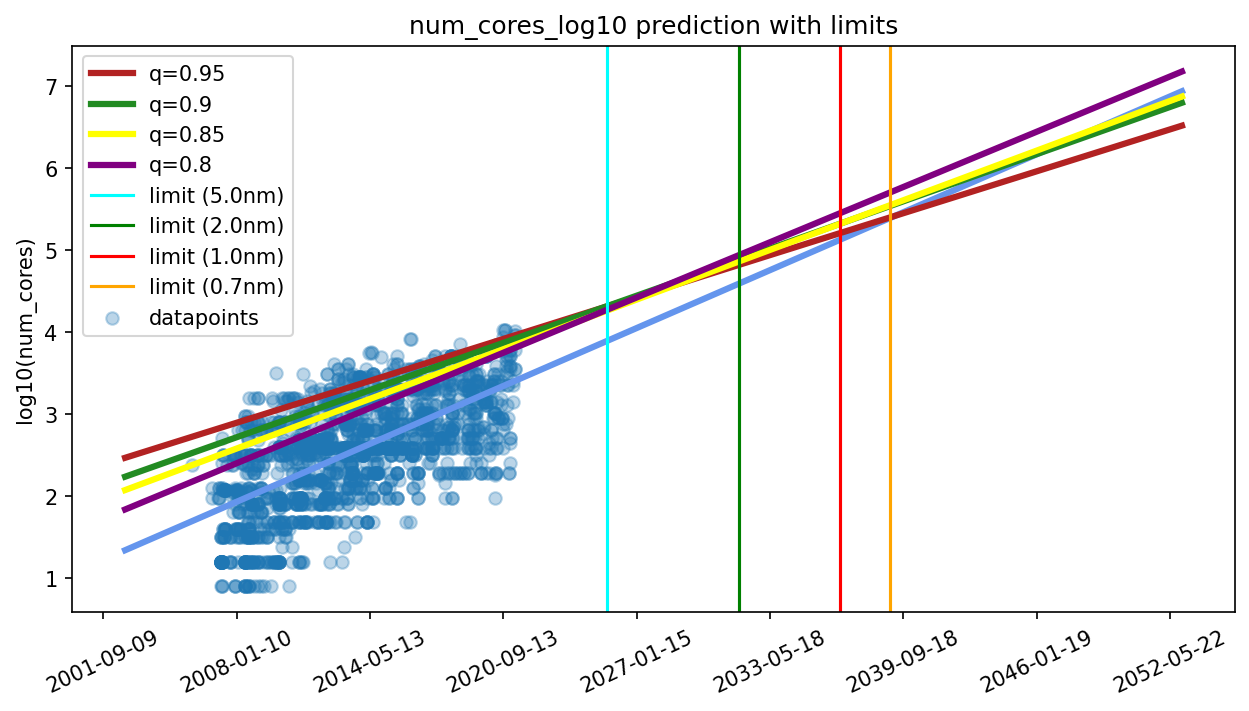
Figure 14: Quantile regressions for the 95th, 90th, 85th and 80th percentile of log10(number of cores) ~ time. The different percentile regressions lead to different slopes of the regression. We have no clear criterion to resolve which is a more accurate extrapolation, and thus, randomly sample from the four different slopes.
All of these considerations are then combined into one prediction for TOP performance with limits.

Figure 15: A distribution over projections of TOP GPU performance. The historical projection comes from a 90th-percentile regression of the dataset. The model predicts that the median dates for the two limits are ~2030 and ~2033 and that the limiting performance is between 1e14 and 1e15 FLOP/s.
Our model predicts that the TOP GPU will hit its physical limit around 2030 and its final limit around 2033. Note that the projection for TOP GPUs (doubling time of 2.69 years) is less steep than for median GPUs (doubling time of 2.34 years). We think this trend is due to the fact that it is already harder to improve current TOP GPUs than a decade ago while the median GPU can still catch up.
We also predict the limits for the median GPU. We find that the median date of the two limits are 2034 and 2039. Furthermore, the model predicts that the maximal performance is between 3e14 and 5e15 and is hit between 2032 and 2044. Note that the maximal performance is higher than for the TOP GPUs which is counterintuitive since the limit should be the same for both approaches. This difference is due to the fact that the slope from current median GPUs is steeper (2.34 years doubling time) than that of TOP GPUs (2.69 years doubling time). Our best guess is that the slope for TOP GPUs is less steep because it has already gotten harder to improve the performance of state-of-the-art GPUs over the last decade and median GPUs still catch up. Thus, we have more confidence in the prediction for TOP GPUs and think that the median projection is an overestimate.
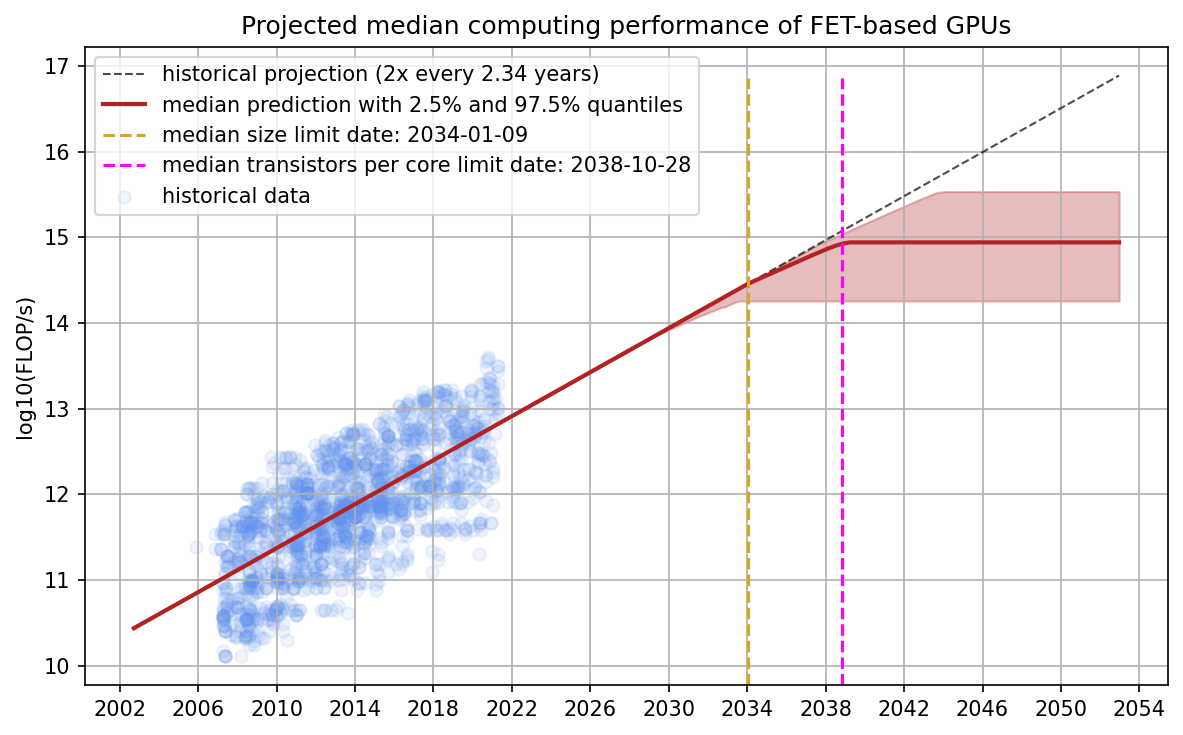
Figure 16: A distribution over projections of the median GPU performance. The historical projection comes from a linear regression of the dataset. The model predicts that the median dates for the two limits are ~2034 and ~2039 and that the limiting performance is between 3e14 and 5e15 FLOP/s.
Lastly, we test if the distinction between MOSFET and FinFET transistors makes a difference for the compute projections. Concretely, one might suggest that FinFET miniaturization has been slightly faster than MOSFET miniaturization, and thus, the limit would be hit earlier.
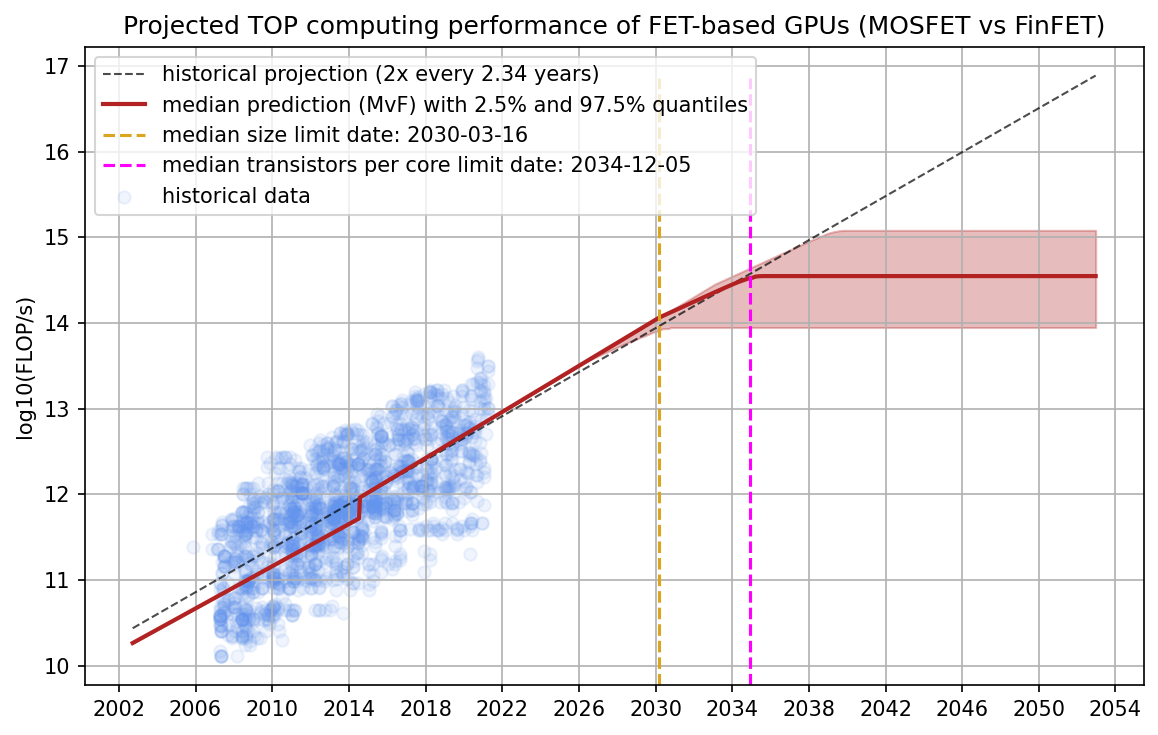
Figure 17: We use a model that takes the MOSFET vs. FinFET distinction of transistors into account. The jump around ~2014-2015 is when the dominant paradigm switched from MOSFET to FinFETs. Since FinFET miniaturization progressed faster in our dataset, the size limit was hit earlier.
We find that the MOSFET vs FinFET distinction results in the limits being hit earlier. However, given that we only have very few data points to fit our model, we are less confident about this prediction. We would cautiously interpret this as mild evidence that physical size limits might be hit earlier than our model would predict since FinFETs are the current paradigm.
Appendix C - Physical size limits of transistors (details)
There have been multiple predictions about the physical size limit of transistors. We have compiled an overview in the following table.
| Paper | Minimum processor size | Limit applies to | Year | Argument |
|---|---|---|---|---|
|
A single-atom transistor | Nature Nanotechnology
See also: Single-atom transistor - Wikipedia |
~0.5 nm (Lattice constant of silicon) Note also that Si5H12, the smallest particle of silicon, has a diameter of 0.43 nm ([Wang et al., 2007]) |
Gate length for any silicon transistor | 2012 | The smallest component on silicon-based chips need to be at least one atom in size. |
| The electronic structure at the atomic scale of ultrathin gate oxides | Nature; Scientists shrink fin-width of FinFET to nearly the physical limit | 0.7 nm | Fin width for FINFET transistor | 2020 | This study achieved a FinFET with sub 1 nm fin width via a bottom-up route to grow monolayered (ML) MoS2 (thickness ~ 0.6 nm) as the fin, which is nearly the physical limit that one can actually achieve |
| Physical limits for scaling of integrated circuits | 3 nm |
Channel/gate4 length for MOSFET transistor |
2010 | According to the state of the art, the minimal length of gate in MOSFET in silicon integrated circuits is around 3 nm. |
| The relentless march of the MOSFET gate oxide thickness to zero | 1.3 nm | Gate width for MOSFET transistor | 2000 | The minimum thickness for anideal oxide barrier is about 0.7 nm. Interfacial roughness contributes at least another 0.6 nm, which puts a lower limit of 1.3 nm on a practical gate oxidethickness |
| A FinFET with one atomic layer channel | <1 nm | Fin width for FINFET transistor | 2020 | Based on this bottom-up fabrication route, the vertical free-standing 2D MLs are further conformally coated with insulating dielectric and metallic gate electrodes, forming a 0.6 nm 𝑊fin ML-FinFET structure |
We choose a limit of 0.7 because this is the size that has been achieved as the fin width of a FINFET transistor in a 2020 prototype. This is only marginally bigger than the size of the silicon atom (0.43nm diameter) and we, therefore, expect that this poses a lower bound or at least a very significant challenge to overcome.
Furthermore, even if you could build transistors at atomic size, there are additional limits to how close you can stack them together, e.g., due to heat or interferences. Therefore, our model includes a distribution over possible size limits.
Appendix D - Process size vs. transistor size
Our dataset reports process size rather than transistor size. Process size seems to be a made-up term that describes something related to, but not exactly the same as, transistor size. Our predictions might have been more accurate if we knew the exact size of the transistor (e.g., the minimum of gate length and fin width) but we find that process size correlates very strongly with these actual physical quantities.
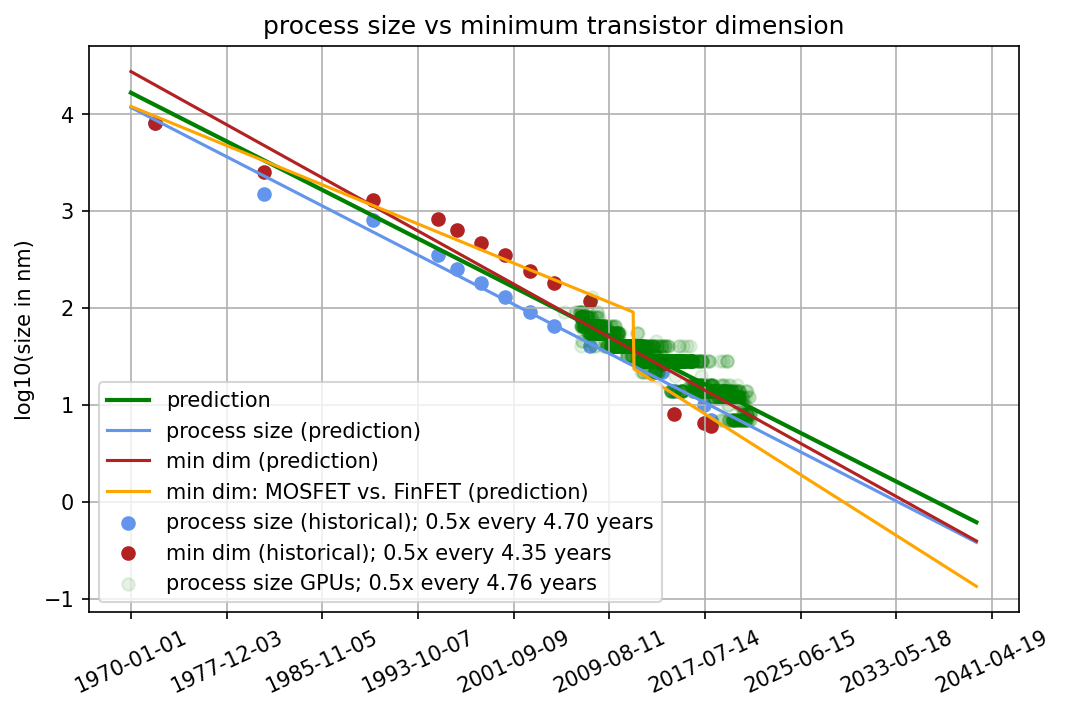
Figure 18: Comparison of process size and minimum transistor dimension. We find that both scale very similarly even when we account for a MOSFET vs FinFET distinction. Therefore, we conclude that we can use process size as a decent approximation for transistor size in the rest of this piece.
Therefore, we will use process size as a proxy for these quantities until we find a more accurate translation. We expect that this assumption introduces some error in our model.
Appendix E - Growth of die sizes
There is a trend toward larger GPUs and die sizes. One could argue that larger die sizes will lead to better performance and thus our predicted limit should be higher. However, we want to argue that a) the increase in die size is a consequence of more cores, and thus, already accounted for in our model, and b) even if the increase in die size wasn’t accounted for, it wouldn’t change the limit by a lot.
Let’s first establish some facts about the growth of different sizes in GPUs. In the following figure, we can see that the average die size increased over time and the upper limit got higher. Furthermore, height and width of the median GPU stayed the same but the maximum increased. For weight, we can see that the variance increased but the average stayed roughly the same. However, height, width and weight are only available for a small subset of the GPUs, so we should be cautious about all interpretations.
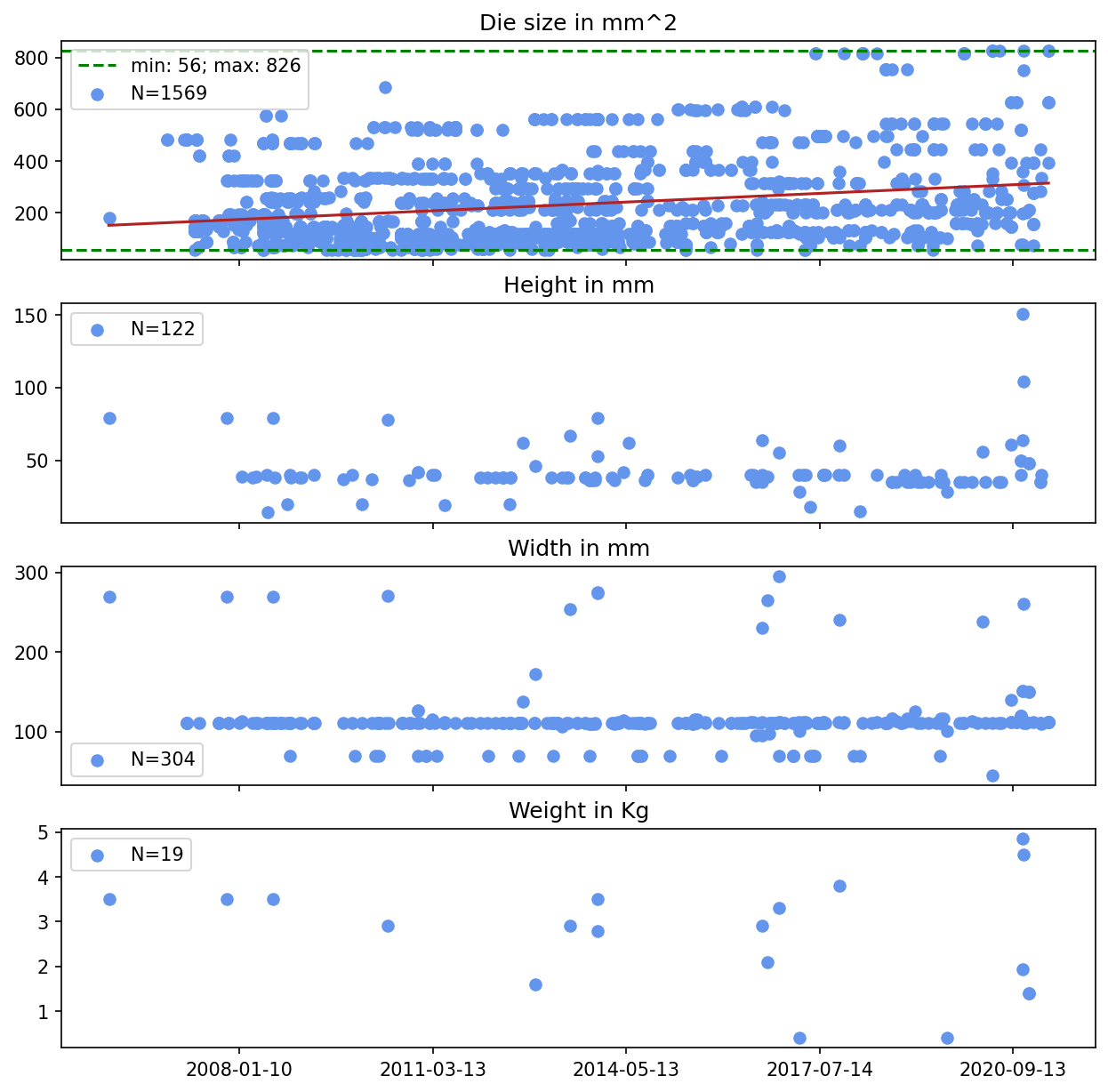
Given the clear trend of increasing die sizes, one might argue that our limit is incorrect because our model doesn’t explicitly incorporate die size. We think there are three important responses to this:
- A key component of our model is the increase in the number of cores and these cores need space. Since the number of cores increases faster than the size of transistors decrease, we think that the growth in die size can be explained entirely by an increase in the number of cores. This trend holds even if you consider the halving time of squared transistor size (because it’s 2D). Concretely, our doubling/halving times (in years) are:
- Doubling time number of cores: 2.70
- Halving time process size: 4.76
- Halving time process size squared: 3.23
- Doubling time number of transistors: 2.68
- Larger GPUs might raise the upper limit of performance for a single GPU, but they don’t raise its price performance. Therefore, the limit of FLOP/s per dollar is still the same, and price performance is ultimately what matters for compute progress.
- Even if larger die sizes were unaccounted for, they wouldn’t raise the limit by a lot. From the above figure, we see that die size has increased by ~2x on average within the last decade and by ~16x from minimum to maximum. So even if we assume that die sizes would grow by, let’s say, another OOM in the next decade, due to Pollack’s rule, we would still only expect a sqrt(10) increase in performance.
To summarize, we expect GPUs to get larger over the coming decade, but we think this is already accounted for in our model. Furthermore, even if it was unaccounted for, it would not lead to a substantial performance increase, and it wouldn’t change the price performance.
Appendix F - Deviations from the current paradigm
There are many deviations from the way GPUs are currently built. These include modifications to the existing paradigm such as 3D chip stacking, specialized hardware, etc. and there are substantially different paradigms such as neuromorphic, analog, optical or quantum computing. In this piece, we will not make any specific predictions about if or when they will replace the current paradigm.
Epoch AI might look into these alternative paradigms in the future and try to get a better understanding of whether they could disrupt the current FET-based architectures.
However, we think there are some reasons to assume that the physical limit poses a relevant boundary and the current way of building GPUs will not just be replaced with something else once we hit the limits. These reasons include:
- The R&D that has already been invested into the current FET-based paradigm is immense. This means that there are highly specialized processes to develop and produce these chips, and the entire pipeline from research to production is much more advanced than with alternative paradigms. Even if the alternative paradigm has the potential to be better, it still requires a lot of time and money to get to a comparable level of sophistication.
- The physical size of the transistor poses a limit for some of the alternative computing schemes as well. Even if we can build chips in 3D rather than 2D, smaller chips still remain one of the core drivers of progress.
We want to emphasize that our expertise on alternative compute schemes and paradigms is limited, and this section should therefore be treated with caution.
Appendix G - Estimates
The exact estimates and goodness of fit metrics for our performance and feature model can be found in the following table.
| Model | Variable (in logs or levels) | coefficients | Standard errors | r-squared | BIC |
|---|---|---|---|---|---|
| log10(FLOP/s) ~ log10(num_cores) + log10(process_size) |
num_cores | 0.9186 | 0.007 | 0.950 | -1753 |
| process_size | -0.3970 | 0.018 | |||
| intercept | 10.0674 | 0.041 | |||
| log10(num_cores) ~ time | time | 0.1113 | 0.003 | 0.411 | 2679 |
| intercept | -221.6495 | 6.241 | |||
| log10(process_size) ~ time | time | -0.0633 | 0.001 | 0.879 | -3743 |
| intercept | 128.8780 | 1.098 |
Table 1: The three subcomponents of our model, i.e., the performance model in the first row and the two feature models below. As you would expect, the number of cores increases over time, process size decreases, and performance increases with more cores and smaller transistors. Furthermore, the model suggests that the number of cores increases faster than the miniaturization decreases and that the number of cores has a larger effect on performance than transistor size. However, since these variables are correlated, these estimates might not reflect the true coefficients, and, in general, a linear regression model should not be mistaken for a causal interpretation.
Time is represented as decimal years, e.g., 2012.5 describes the 365/2-th day in 2012. We find that, as you would expect, the number of cores increases over time, process size decreases over time and performance increases with more cores and smaller transistors.
-
In recent years, chip manufacturers have chosen to report a quantity called “process size” rather than the actual minimal width of a transistor (such as fin width or gate width). ↩
-
We assume that future GPUs roughly have the same size as today’s GPUs. If the size of the GPU grows by 10x, then you can fit 10x more cores into it without any changes in transistor size or the number of transistors per core. However, we don’t expect that incorporating increasing die sizes changes our predictions much; see Appendix E. ↩
-
Of course, the amortization period might be longer than three years once miniaturization is exhausted, as when this happens, we should expect longer replacement cycles, which would incentivize longer usage of state-of-the-art GPUs. ↩
-
Note that the channel length and gate length are usually roughly similar in size (source). ↩